1. 서 론
2. 자료 및 방법
3. Sa와 Ssa분조의 평형조석 이론식과 두드슨 전개식
4. 결과 및 토의
4.1 분석 기간에 따른 Task2K와 UTide 간 Sa 지각 차이와 조위 예측
4.2 분석자료 길이에 따른 Sa 조화상수의 안정도
4.3 해역별 Sa 조화상수 분포 특성
4.4 월평균 해수면, Sa와 Ssa의 합성 조위, 대기압 보정 해수면, 비부피 높이 간 관계
5. 결 론
1. 서 론
우리나라 연안에서 해수면은 대기압, 바람, 해표면 가열, 해류, 파랑, 강물 등에 의해 뚜렷한 계절 변동성을 보인다. 1년 이상 해수면 높이 자료의 조석 조화분해 시에 산출되는 태양 연주조(solar annual tide)인 분조와 태양 반년주조(solar semi-annual tide)인 는 장주기 비천문조(non-astronomical tide 또는 non-equilibrium tide)로, 달과 태양의 인력(gravitational forcing)에 의한 영향이 매우 작다. 해수면의 계절변화 폭은 해 마다 다른 해양·기상학적 과정(processes)에 의해 크게 영향을 받기 때문에 매년 변화한다(Pugh, 1987). 특히 분조의 영향이 상대적으로 큰 해역의 경우에 이처럼 연변동(annual variation)이 비교적 큰 분조를 조위 예측에 고려할 때 보다 적절한 조화상수 값을 사용할 수 있다면 특정 해의 조위 예측 정확도를 좀 더 향상시킬 수 있을 것이다. 하지만 지금까지 조위 예측과 관련하여 주요 조화분해 프로그램 간 계산식과 산출 결과 차이, 해수면의 연변동에 있어서 의 역할에 관해 자세히 살펴 본 연구는 없다. 한편 Kang et al.(2008)은 우리나라 주변해의 조화상수의 공간 분포를 조사하여, 이 변동성이 계절에 따른 해수의 비부피(specific volume)와 대기압의 변화에 의해 크게 영향을 받는다고 주장하였다. Ko et al.(2016)은 동해안과 같이 분조가 주요 4대 분조(M2, S2, K1, O1) 만큼 진폭이 큰 해역의 경우, 조석 기준면 결정 시에 분조에 대한 고려가 필요하다는 사실을 지적하였다.
2020년 현재 국립해양조사원은 우리나라 연안에 위치한 120개 지점에 대한 조석표를 간행하여 제공하고 있다. 조석표 간행을 위해 55개의 상시 조위관측소와 65개의 임시 조위관측소에서 기본적으로 1년 이상 관측한 해수면 높이 자료를 사용한다. 다음 해 조석표 발간을 위해서, 상시 조위관측소 예보조화상수의 경우 보통 전년도 전체 1년간의 상시 조위관측소 관측자료를 조화분해한 후 그 결과를 전년에 사용한 조화상수와 비교하여 사용유무를 판단한다. 즉, 매년 6월경에 전년도에 상시 조위관측소에서 1년간 관측한 자료를 조석 조화분해한 결과 중 M2 지각이 기존 조위예측에 사용된 M2 지각에 비해 2.4°(서·남해안) 또는 4.8°(동해안) 이상 차이가 날 경우에 기존 예보조화상수를 전년도 예보조화상수로 대체하여 다음 해의 일별 고조와 저조 예측정보를 산출하여 조석표에 수록하고 있다. 임시 조위관측소의 경우에도 일반적으로 1년 관측자료가 조화분해에 사용되지만 관측의 용이성 때문에 관측 시작일이 보통 3월 이후로 다음 해까지 이어진 자료가 분석에 사용된다. 이처럼 분조의 조화상수는 특정 해에 산출된 값이 조위 예측에 사용된다. ‘조석 조화분해에 사용되는 1년 이상 관측자료의 시작 시기와 길이에 따라 조화상수 값이 정량적으로 얼마나 영향을 받을까?’라는 궁금증이 이 연구를 시작하게 된 동기이다.
이 연구에서는 (1) 인천 조위관측소에서 19년간 장기 관측한 해수면 높이 자료를 사용하여 두 종류의 잘 알려진 공개용 조석 조화분해 프로그램으로 분조를 산출한 후 조화상수 값을 비교하였으며, 특히 조화상수 중 지각 값의 차이가 크게 발생하는 주요한 이유에 관해 조사하였다. 또한, (2) 분석에 사용되는 관측 자료의 시작 시각과 길이에 따른 조화상수 값의 변동성을 조사하였으며, 이로부터 조석표 작성에 있어서 분조에 의한 조위 예측 오차를 최대한 줄일 수 있는 조석 조화분해에 사용할 적정 관측자료 길이에 대한 길잡이를 제시하였다. 또한, (3) 우리나라 해역별 조화상수 분포 특성을 살펴보았으며, 이러한 공간 분포 특성을 가지는 원인에 관해 논의하였다. (4) 우리나라 해역에서 월평균 해수면의 비대칭적 계절 변화를 일으키는데 있어서 분조와 반년주조인 분조가 기여하는 정도에 관해서도 살펴보았다. 끝으로, (5) 월평균 해수면, 대기압 보정 월평균 해수면, 비부피 높이 간의 관계로부터 해수면의 해해변화(year to year variation) 요인을 살펴보았다.
2. 자료 및 방법
우리나라 연안에 위치한 21개 조위관측소(Fig. 1)에서 19년(1999-2017년) 동안 관측된 1시간 간격의 해수면 높이 자료를 각각 연별로 369일 자료 세트(set)를 만들어 각각 조석 조화분해하여 분조의 조화상수를 산출하였다. 즉, 19년 동안 매년 1월 1일 0시 0분에 시작하여 369일 간의 자료를 조석 조화분해하였다. 이 369일 간의 자료 길이는 실질적으로 모든 짧은 주기 분조들(the short period constituents)의 합주기(synodic period)의 배수와 매우 가까우며, 계절 기상 영향을 제거하는 데 적합한 분석 표준 길이이다(Schureman, 1958; Dronkers, 1964). 아울러 분조의 해역별 중요도를 알 수 있도록 보통 가장 우세한 분조로 알려진 분조의 조화상수도 연별로 산출하여 분석하였으며(결과 제시하지 않음), 해수면의 비대칭적 계절 변화에 영향을 미치는 분조의 분포 특성을 살펴보고자 분조의 조화상수도 연별로 산출하였고 분조의 비대칭 정도 계산에 사용하였다.
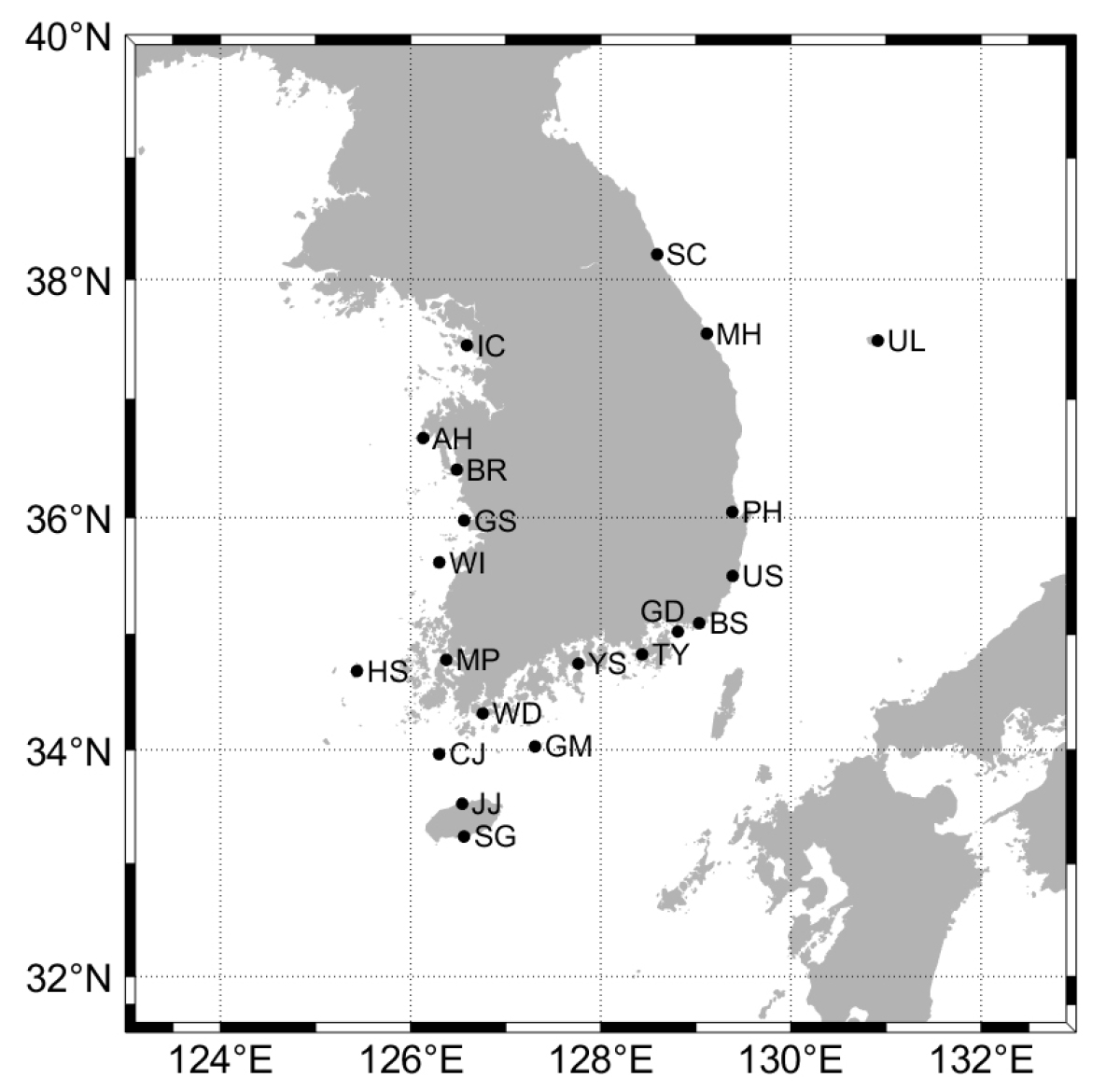
Fig. 1.
Locations of the 21 tidal observation stations referred to in this study, along the west, south and east coasts of Korea, Jejudo and Ulleungdo. See Table 1 for the full tidal observation station names.
또한 인천 조위관측소만을 대상으로 20년(1999-2018년) 자료를 19년간 일별로 이동하면서 369일 자료 세트를 조석 조화분해하여, 관측시기에 따른 분조 조화상수의 안정도를 살펴보았다. 즉, 1999년 1월 1일부터 1일 간격으로 날짜를 변경하면서 2017년 12월 27일까지 6936개의 369일 관측자료 세트들을 생산한 후 각각 조석 조화분해하였다. 조석 조화분해 입력자료로 국립해양조사원의 1차 자동 품질처리(시간, 전원, 이상 값, 지역·계절적 한계범위 등 검사)와 2차 수동 품질처리(조화상수 변동성 분석, 잔차 분석, 시계 오작동 보정, 인근 조위관측소 자료와 비교, 결측 구간 보간, 기준면 변동 검사 등)를 거친 해수면 높이 관측자료를 사용하였다(KHOA, 2019). 조석 분석에 사용한 조석 조화분해 프로그램은 전 세계적으로 조석 조화분해·예측에 널리 사용되고 있는 TASK2K package (Bell et al., 1999)와 장기 연속 조석 조화분해·예측이 가능한 MATLAB 소프트웨어 기반의 UTide (Codiga, 2011)를 사용하였다. 이 UTide는 캐나다 IOS tidal package (Foreman, 1977)와 T_TIDE (Pawlowicz et al., 2002)를 기반으로 하고 있으며, 조석 조화분해는 ‘ut_solve.m’를 사용하고 조석 예측은 ‘ut_reconstr.m’을 사용한다. ‘ut_solve.m’로 분조별 조석 조화상수를 구할 때 기본으로 지정(default)되어 있는 ‘반복적 가중의 최소자승법(iteratively reweighted least-squares, IRLS)’에 코시 가중함수(Cauchy weight function)와 2.385의 조정 매개변수(tuning parameter) 값을 사용하였다. Fortran 기반의 TASK2K 프로그램의 경우, 조석 조화분해에 ‘tira.f’를 사용하고 조석 예측에 ‘marie.f’를 사용한다. ‘tira.f’에서는 조석 조화상수를 구할 때 선형 연립방정식의 해를 구하는 방법으로 ‘가우스-자이델 방법(Gauss-Seidel method)’을 사용한다.
3. Sa와 Ssa분조의 평형조석 이론식과 두드슨 전개식
평형 조석(equilibrium tide theory) 이론에서 지구가 태양(엄밀히 말해, 태양과 지구의 공통질량 중심) 주위를 공전할 때 분조가 지구와 태양 사이의 거리 변화와 관련 있다면, 분조는 이에 따른 태양 적위 변화와 관련이 있다. 지구가 태양 주위를 공전할 때 지구와 태양 사이의 거리가 변하며, 지구의 자전축이 지구 공전 궤도면에 직각인 직선을 기준으로 23.45° 기울어진 채로 공전한다. 이와 같이 지구가 공전할 때 태양의 인력과 원심력의 차이를 수식으로 표현한 것이 분조와 분조이다. 임의 시각 t에 대한 와 분조의 조위 계산식은 각각 다음과 같이 표현할 수 있다(Pugh and Woodworth, 2014).
여기서, 는 태양의 평균 경도(mean longitude of the Sun)로 춘분점과 추분점에서 0°이며, 는 근일점의 평균 경도(mean longitude of the solar perigee)이고, 는 지구상의 위도이다. 이들 식으로 계산된 와 분조는cm 단위이다. 식 (1)과 (2)로부터 계산된 와 분조의 진폭 모두 위도 35° 16′N(S)에서 0 cm의 값을 갖는다. 또한 북극과 남극에서 와 의 진폭은 각각 0.31 cm와 1.95 cm으로 최댓값을 가지며, 적도에서는 각각 그 절반인 0.155 cm와 0.975 cm를 갖는다(Fig. 2a,b). 분조의 진폭이 분조의 진폭에 비해 최대 6.29배 정도 더 크다. 또한 2가 0°인 춘분(3월 21일경)과 추분(9월 23일경)일 때, 평형 조석 이론에 의한 분조의 조위는 최댓값을 가진다. 식 (1)의 오른쪽 코사인 항에서 연간 변화율이 0.0172° yr-1로 아주 작은 값(2020년 1월 1일에 283.2838°)을 에서 빼줌으로서 매년 초에 가 3°내외로 0°에 가까운 값을 갖도록 해준다. 나아가 조석에 반응하는 지구의 탄성 반응을 특징짓는 무차원 매개변수인 ‘Love number’로 불리는 ‘감소 계수(diminishing factor)’ 0.69를 평형 조석 이론으로 구한 진폭에 곱하면 와 진폭 값 모두 그 만큼 줄어들게 된다(Fig. 2a,b).
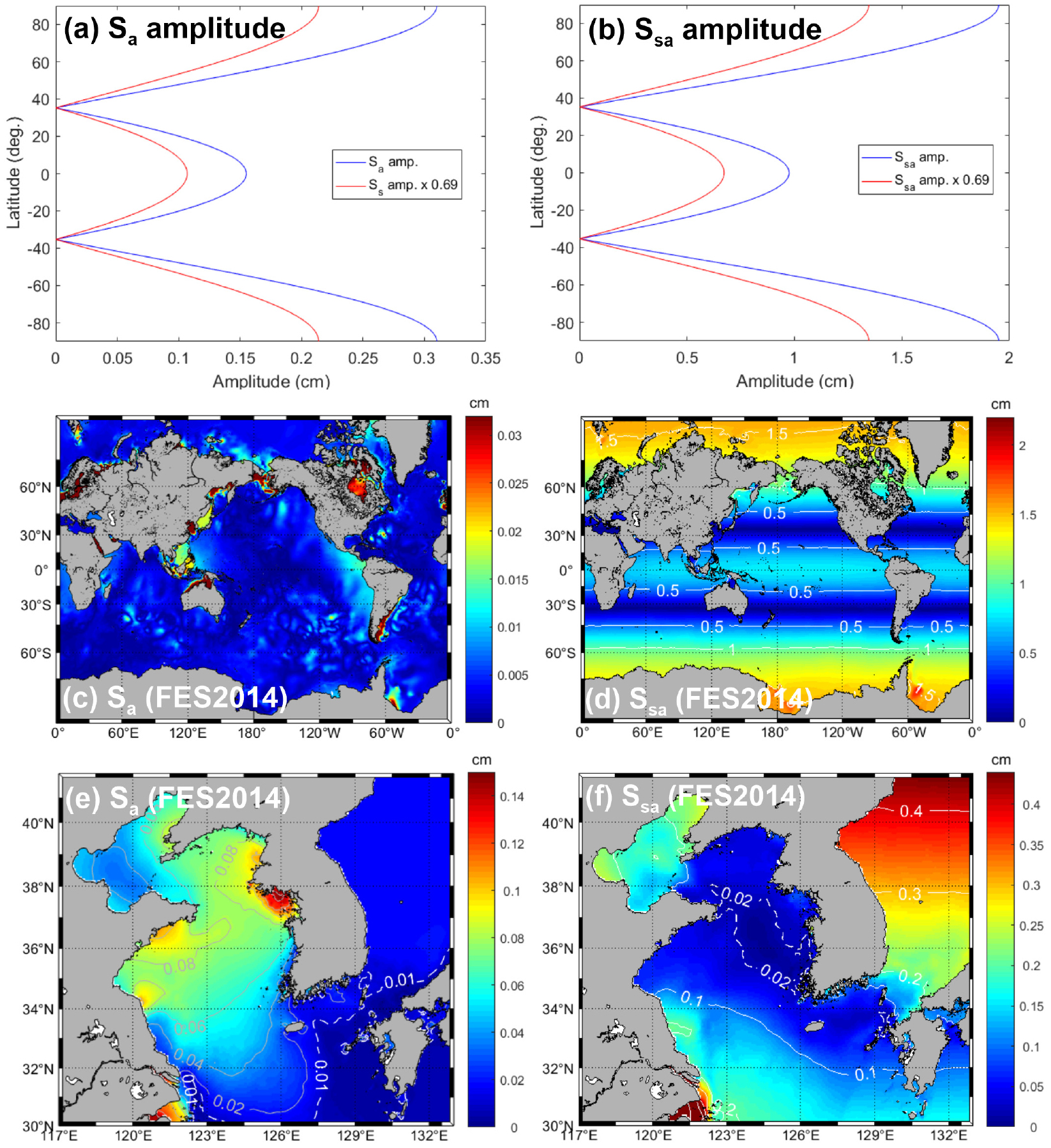
Fig. 2.
The theoretical amplitudes of the (a) and (b) constituents for each latitude, calculated based on Equilibrium Tide Theory (i.e., Eqs. 1 and 2). The original amplitudes are in blue while those multiplied by the diminishing factor (0.69) are in red. Global distribution of (c) and (d) amplitudes derived from FES2014 tide model data and (e, f) those derived for the marginal seas around Korea.
또한 인공위성으로 관측한 해수면 높이 자료를 동화한 전 지구 조석 수치모델로부터 산출된 FES2014 (Carrère et al., 2016)의 와 분조의 진폭 분포를 살펴보면, 분조의 진폭(Fig. 2c)은 공간적으로 불규칙하며 식 (1)로 구한 값(Fig. 2a)보다 한 차수(order) 이상 작으나, 분조의 진폭(Fig. 2d)은 대체로 식 (2)로 구한 값(Fig. 2b)과 매우 유사한 분포를 보인다. 이처럼 FES2014에서 제공하는 분조의 진폭이 불규칙한 분포를 보이는 이유는 평형조석 이론이 모델에 적용되어 직접 계산된 결과가 아니라 S2와 T2, K1과 S1, S2와 R2 등의 분조들 간 비선형 상호작용(nonlinear interaction)에 의해 생성된 결과이기 때문이다(프랑스 AVISO에 전자우편으로 문의한 결과임). 특히, 우리나라 주변 해역에서 태양 인력에 의한 와 분조의 진폭은 각각 0.2 cm 미만과 0.5 cm 미만으로 작다. 황해에서는 진폭이 진폭보다 0.05 cm 이상 약간 더 큰 반면에, 동해에서는 진폭이 진폭보다 한 차수 더 크다(Fig. 2e,f).
그러나 실제 우리나라 연안에서 관측된 진폭은 10.5~18.6 cm로 태양 인력 변화에 의한 성분에 비해 100배 이상 크고(Table 1), 울산 조위관측소( 진폭은 평균 15.5 cm임)를 제외한 동해안 조위관측소(포항, 묵호, 속초, 울릉도)에서는 진폭(평균 3.3~6.8 cm)보다 오히려 4.4~8.2 cm 더 크다. 진폭은 평균 0.6~2.4 cm로 평형 조석 분조보다 최대 5배 크지만 분조에 비해 한 차수 정도 작다(Table 2). 따라서 이 결과로부터 진폭은 태양 복사의 연변화 성분(radiational annual variation component)에 큰 영향을 받고 태양 인력(gravitational forcing)의 연 변화 영향은 상대적으로 작게 받는다는 것을 알 수 있다.
Table 1.
and tidal harmonic constant statistics (annual means and standard deviations) derived from tidal harmonic analyses of hourly sea-level observation records (1999 to 2017) observed at 21 tidal stations along the Korean coast, calculated using UTide (Codiga, 2011) and Task2K (Bell et al., 1999). The asymmetric factors (amplitude ratios and relative phase lag differences) are calculated from the Task2K results
| Region | Tidal station | UTide (Codiga, 2011) | Task2K (Bell et al., 1999) | Asymmetry factor | |||||||
| (cm) (mean±std) | (°) (mean±std) | (cm) (mean±std) | (°) (mean±std) | (cm) (mean±std) | (°) (mean±std) | (cm) (mean±std) | (°) (mean±std) | (°) | |||
| West Coast |
IC (Incheon) | 18.6±1.7 | 212±6 | 1.7±1.3 | 345±141 | 19.5±1.6 | 134±6 | 1.8±1.4 | 351±135 | 0.092 | 276 |
|
AH (Anheung) | 17.7±1.7 | 213±6 | 1.3±1.1 | 331±119 | 18.7±1.6 | 134±6 | 1.4±1.2 | 339±119 | 0.076 | 290 | |
|
BR (Boryeong) | 18.6±1.7 | 212±5 | 1.5±1.2 | 319±100 | 19.5±1.7 | 134±5 | 1.5±1.2 | 325±101 | 0.078 | 303 | |
|
GS (Gunsan) | 18.1±2.1 | 213±7 | 1.7±1.5 | 335±125 | 18.6±2.2 | 135±7 | 1.9±1.5 | 338±133 | 0.100 | 293 | |
|
WI (Wido) | 16.6±2.2 | 214±7 | 0.6±1.6 | 314±108 | 17.1±2.1 | 136±6 | 0.6±1.5 | 319±110 | 0.036 | 313 | |
|
MP (Mokpo) | 18.2±2.0 | 219±7 | 2.2±1.5 | 326±113 | 18.0±2.0 | 142±7 | 2.2±1.5 | 326±113 | 0.124 | 318 | |
|
HS (Heuksando) | 15.0±1.7 | 218±7 | 1.3±1.4 | 332±130 | 15.5±1.7 | 140±7 | 1.4±1.5 | 335±131 | 0.092 | 305 | |
| South Coast |
CJ (Chujado) | 15.7±2.0 | 224±9 | 1.3±1.9 | 355±120 | 15.8±2.0 | 148±8 | 1.5±1.8 | 353±125 | 0.096 | 302 |
|
JJ (Jeju) | 17.5±1.6 | 225±6 | 1.6±1.6 | 4±135 | 17.6±1.7 | 148±5 | 1.8±1.5 | 0±144 | 0.103 | 296 | |
|
SG (Seogwipo) | 16.0±1.7 | 227±9 | 2.1±1.8 | 3±144 | 16.2±1.8 | 150±9 | 2.4±1.8 | 0±151 | 0.146 | 300 | |
|
WD (Wando) | 15.8±1.7 | 222±6 | 1.8±2.0 | 358±140 | 16.0±1.8 | 145±6 | 2.0±1.9 | 352±142 | 0.127 | 298 | |
|
GM (Geomundo) | 14.8±1.7 | 224±7 | 1.8±1.6 | 341±138 | 14.9±1.8 | 148±7 | 2.1±1.6 | 339±139 | 0.138 | 317 | |
|
YS (Yeosu) | 16.2±2.1 | 222±7 | 1.8±1.6 | 346±133 | 16.2±2.0 | 145±7 | 1.9±1.6 | 343±136 | 0.118 | 307 | |
|
TY (Tongyeong) | 13.8±1.7 | 223±7 | 1.3±1.5 | 343±125 | 13.8±1.7 | 147±7 | 1.5±1.5 | 341±129 | 0.107 | 313 | |
|
GD (Gadeokdo) | 13.4±1.7 | 223±7 | 1.6±1.4 | 334±122 | 13.5±1.7 | 147±7 | 1.8±1.4 | 333±117 | 0.135 | 320 | |
|
BS (Busan) | 10.7±1.7 | 221±9 | 1.1±1.3 | 320±119 | 10.9±1.7 | 145±8 | 1.4±1.3 | 323±115 | 0.133 | 328 | |
| East Coast |
US (Ulsan) | 10.7±2.0 | 221±14 | 1.2±1.3 | 302±104 | 10.6±2.0 | 146±14 | 1.5±1.3 | 307±107 | 0.138 | 344 |
|
PH (Pohang) | 11.0±2.0 | 222±9 | 1.2±1.2 | 293±73 | 11.0±2.0 | 146±9 | 1.4±1.2 | 300±98 | 0.125 | 351 | |
|
MH (Mukho) | 10.5±1.5 | 219±11 | 1.6±1.2 | 251±71 | 10.4±1.5 | 143±11 | 1.5±1.2 | 257±78 | 0.146 | 28 | |
|
SC (Sokcho) | 11.7±1.4 | 217±9 | 1.5±1.1 | 251±58 | 11.6±1.4 | 140±9 | 1.5±1.2 | 256±63 | 0.125 | 25 | |
|
UL (Ulleungdo) | 13.0±5.9 | 234±31 | 2.4±1.7 | 149±76 | 12.1±5.9 | 164±31 | 2.3±1.6 | 148±77 | 0.193 | 181 | |
Table 2.
Comparison of the values associated with the and constituents in UTide and in Task2K
식 (1)에 표현된 분조에 의한 조위 변화는 일반적으로 조석 조화분해·예측 프로그램에서 사용되는 두드슨 전개식(Doodson’s development)을 사용하여 다음과 같이 표현할 수 있다.
여기서, 와 는 분조의 평균 진폭과 지각이며,는 천문 위상각(astronomical argument)이다. 조화상수 와 를 구하는 절차는 간단히 다음과 같다. 먼저 분석할 특정 해의 1년 해수면 높이 관측자료의 시작 시각()을 기준 시(00:00)로 한 자료를 최소제곱근사법(least-squares fitting) 등을 사용해 분조에 대한 진폭()과 지각()을 구한다. 태양과 관련된 장주기 분조의 경우 진폭과 지각에 대해 18.61년 주기를 갖는 달의 교점 보정(nodal modulation correction)이 필요 없기 때문에 간단히 는 바로 가 되며, 에 를 더해주어 가 된다. 조화분해 시에는 값을 에 더해주고, 조위 예측 시에는 에서 값을 빼주는 과정이 이론적으로 자료분석 시작 시기에 상관없이 지각 값을 일정하게 만들어 준다(Byun, 2007).
는 6개의 천문변수들()과 이에 대응하는 정수형 계수들로 이루어진 두드슨 수(Doodson numbers) 즉, () 간 곱으로 다음과 같이 표현할 수 있다.
여기서, ()는 각각 (0,0,1,0,0,–1)이다. 식 (3)에서 일 때, 식 (3)의 코사인(cosine) 함수 변수(argument)는 식 (1)의 코사인 함수 변수와 같다.
식 (2)의 분조에 대한 도 이와 같은 방법으로 두드슨 수를 이용하여 다음과 같이 표현할 수 있다.
여기서, ()는 각각 (0,0,2,0,0,0)이다.
식 (4)의 계산식에는 항이 들어가 있는 반면에 식 (5)의 계산식에는 이 항이 없다는데 주목할 필요가 있다. 참고로 UTide와 Task2K에서 사용하고 있는 천문변수들()의 계산식은 Appendix A1 (Table A1)에 제시하였다.
4. 결과 및 토의
4.1 분석 기간에 따른 Task2K와 UTide 간 Sa 지각 차이와 조위 예측
인천 조위관측소에서 20년(1999-2018년) 간 한 시간 간격으로 관측한 해수면 높이 자료를 하루씩 이동하면서 구성한 6936개의 1년(369일) 자료 세트들을 Task2K와 UTide의 조석 조화분해 프로그램으로 각각 조석 조화분해하여 분석 기간에 따른 이 두 프로그램 간 분조의 조화상수 결과(Fig. 3)를 살펴보았다. 먼저 Task2K로 계산된 전체 진폭과 지각에 대한 각각의 평균과 표준편차는 19.7±1.8 cm와 133.1±5.4°이었다. 진폭의 범위는 15.5~24.7 cm로 9.2 cm의 변화 폭을 보였으며, 지각의 범위는 120.0~144.5°로 24.5°의 변화 폭을 보였다. 한편 UTide로 계산된 결과의 경우, 전체 진폭과 지각에 대한 각각의 평균과 표준편차는 18.7±1.9 cm와 211.7±5.6°이었다. 진폭의 범위는 14.8~24.0 cm로 9.2 cm의 변화 폭을 보였으며, 지각의 범위는 198.5~224.0°로 25.6°의 변화 폭을 보였다(Fig. 3a,b). 이들 결과는 몇 개월 인접 기간에 동일한 길이의 해수면 자료를 분석에 사용했음에도 불구하고 자료 세트의 구성 시기에 따라 조화분해된 조화상수가 불규칙적인 변동성을 갖는다는 사실을 잘 보여준다. 즉, 조화분해에 사용된 관측자료의 시작과 끝 시기에 따라 조화분해 결과로 얻어지는 조화상수가 크게 달라짐을 알 수 있다. 또한 Task2K를 이용하여 구한 진폭에서 UTide를 이용하여 구한 진폭을 빼면 –0.01~1.83 cm이었고, 그 평균(편향)과 표준편차는 1.0 cm와 0.3 cm이었다. 이처럼 이 두 프로그램의 진폭 차이가 평균적으로 1 cm 이상 나는 주된 이유는 조석 조화상수를 구하는 방법이 다르기 때문이다. 제2장에서 언급했듯이, UTide (ut_solve.m)는 극단치(outlier)의 영향을 크게 받지 않는 견고한(robust) 방법인 IRLS(코시 가중함수)를 사용한 반면에 Task2K (tira.f)는 선형 방정식의 해를 푸는 극단치의 영향을 더 받는 가우스-자이델 방법을 사용하기 때문이다(Codiga, 2011). 이와 관련한 추가적인 실험과 그 결과는 Appendix A2를 참고하기 바란다.
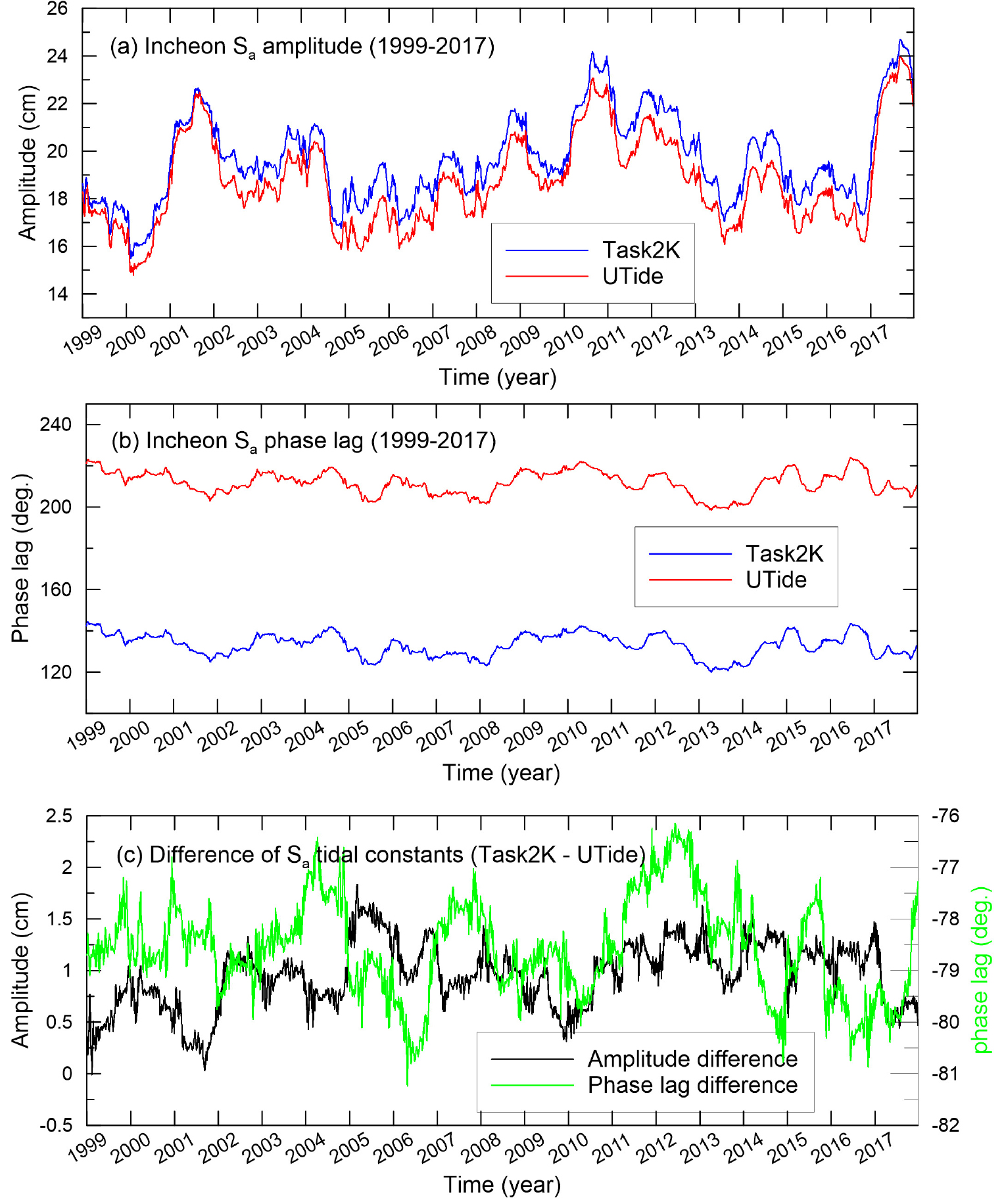
Fig. 3.
The daily amplitudes (a) and phase lags (b) of the constituent at Incheon Tidal Station, calculated from 369 day data slices of the 19 year Incheon sea level record using Task2K (blue line) and UTide (red line). Note that the first data slice began January 1, 1999, with each subsequent slice starting 24 hours after the first start date, until the final slice starting December 27, 2017). (c) Differences between the Task2K and UTide amplitude and phase lag results shown in (a) and (b).
반면에 지각 차의 범위는 –81.2~–76.2°이었으며, 그 평균(편향)과 표준편차는 –78.6°와 0.9°로 편향에 큰 차이를 보였다(Fig. 3c). 이처럼 큰 지각 차이로 인한 조위 예측 값의 차이를 알아보기 위해, UTide ‘ut_reconstr.m’과 Task2K ‘marie.f’의 각 조석 예측프로그램에 인천 조위관측소의 19년(1999-2017년) 동안 연별로 벡터 평균(vector average)한 분조의 조화상수 값만을 사용하여 2020년 1년간 조위를 1시간 간격으로 예측하였다. 즉, UTide와 Task2K를 이용한 조위 예측에 분조의 조화상수 값으로 각각 18.6 cm, 212°와 19.5 cm, 134°를 사용하였다(Table 1). 여기서 사용한 벡터 평균법은 다음과 같다. 먼저 연별로 구한 모든 해당 분조의 진폭과 지각을 극좌표계에서 벡터의 길이와 각도로 표현한다. 이 벡터들을 다시 직각좌표계 상에서 x-방향 성분과 y-방향 성분 값으로 기록한다. x-방향 성분과 y-방향 성분 값들을 각각 평균하여 평균값을 구하고, 이 평균 벡터를 다시 극좌표계에서 벡터의 길이와 각도(진폭과 지각)로 변환하여 조석 조화상수를 구하는 방법이다(Byun et al., 2019). 이 두 프로그램들로 예측한 분조에 의해 예측 조위는 Task2K가 UTide보다 최댓값과 최솟값 모두 1일 이내에서 약간 더 빨리 나타났으며, 최댓값과 최솟값은 각각 1.09 cm 정도 더 크거나 작게 예측되었다(Fig. 4). 이들 1년 예측 조위는 두 프로그램 간 19년 평균 의 진폭(△1 cm)과 큰 지각(△78°) 차이에도 불구하고, 거의 이들 진폭 차이에 해당하는 ±1.09 cm 범위에서 조위 차이를 보였다.
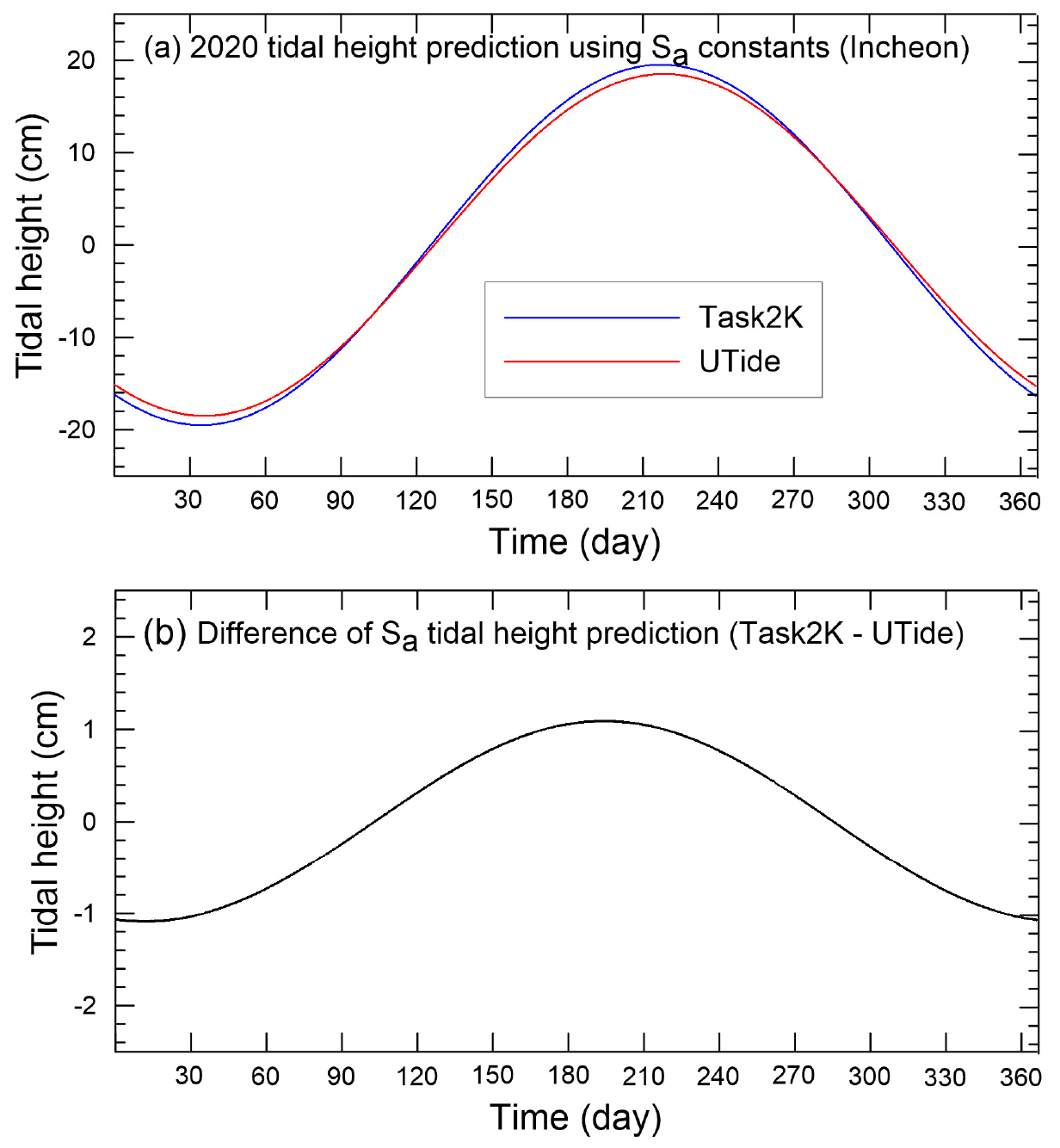
Fig. 4.
(a) Comparison of 2020 Incheon Tidal Station tidal height predictions produced based on constants and calculated using Task2K (blue line) versus UTide (red line), and (b) their difference. See Table 1 for values of the Incheon constants.
이처럼 두 조석 조화분해프로그램 간 지각 차가 큼에도 불구하고 매시간 예측된 조위들의 차가 크지 않은 이유가 무엇인지 자세히 살펴보고자 한다. 식 (4)의 시간()에 따라 변하는 는 기준 시각()의 값에 로부터 경과한 시간()을 각속도()에 곱한 값을 더한 다음 식으로 표현할 수 있다.
식 (6)을 식 (3)에 대입하면 다음과 같이 표현할 수 있다.
UTide와 Task2K에서 분조에 의한 조위를 예측할 때 사용되는 의 계산식으로, UTide는 식 (4)를 사용한 반면에, Task2K에선 식 (6)을 사용한다는 점에서 차이가 있다. 하지만, 식 (4)와 식 (6)은 표현 상 다를 뿐 결과적으로 같은 식이다. 따라서 이들 조석 조화분해 프로그램 간 분조의 지각 차이는 계산식과 밀접한 관련이 있다. UTide에서는 를 구하기 위해 Table A1에 제시된 6개의 천문변수들(astronomical variables: ) 각각에 대응하는 (0,0,1,0,0,–1)의 두드슨 수들을 곱한 결과인 다음 식을 사용한다(Godin, 1972).
이 식은 받아드려진 국제 관행이다(Zetler et al., 1985). 식 (8)의 오른쪽 항에서 연간 변화율이 0.0172° yr-1로 아주 작은 값(2020년 1월 1일에 283.2838°)을 에서 빼줌으로서 매년 초에 가 3° 내외로 0°에 가까운 값을 갖도록 해준다.
반면에, Task2K에서는 가 평형 조석보다 기후에 의한 평균 계절(climate-driven average seasonal) 해수면 변동을 나타낸다는 측면에서 기상조(meteorological tides)로서 더 중요하다는 점에 착안하여 에 대응하는 두드슨 수를 0으로 두어서, 좀 더 단순하게 두드슨 수(0,0,1,0,0,0)를 각 해당 천문 변수에 곱해서 다음 식을 사용한다(Zetler et al., 1985; Pugh, 1987; NOAA, 2009).
이처럼 UTide와 Task2K 간 지각 값의 차이와 시간에 따른 지각 차이의 미세한 변화(각속도의 차이)는 궁극적으로 20,942년 주기로 변하는 태양의 근일점 변화와 관련된 항의 고려 유무와 직접적으로 관련이 있다. 예를 들어, 를 2000년 1월 1일 0000시로 가정하면, 식 (8)로 계산한 UTide의 는 358.03°인 반면에, 식 (9)로 계산한 Task2K의 는 279.97°이므로(Table A1), 이 두 조석 조화분해 프로그램 간 에 대한 조석 조화분해 결과가 대략 78° 차이가 나는 이유를 설명할 수 있다. 즉, 이들 프로그램 간 지각 계산 값의 근본적 차이는 항 값의 고려 유무에 따라 발생한다. 또한, 는 100년에 약 1.719°로 아주 작게 변한다는 점을 고려하여 Task2K의 조석 조화분해·예측 프로그램에서는 일관성 있게 이 항을 고려하지 않고 있다. 그러므로 이들 산출 지각을 해석할 때 유의해야 한다. 예를 들어, 두 조화분해 프로그램에서 산출된 지각 값이 0°라고 했을 때, Table 2에 제시된 이들 해당 시작일의 값과 프로그램 간 차이에서 유추할 수 있듯이 UTide의 경우 분조에 의해 연초에 해수면이 가장 높은 것을 의미하는 반면에, Task2K의 경우에는 분조에 의해 춘분일(spring equinox) 근방에서 해수면이 가장 높은 것을 의미한다(Bell et al., 1999). 따라서 UTide처럼 계산 시에 항 값을 고려한 경우 어느 1월 1일에 계산된 의 값이 360° (0°)에 가까운 값을 가지므로, 산출된 지각 결과로부터 직관적으로 연중 변화가 최대인 시기를 파악하기 쉽다. 반면에, 와 의 관계에서 모든 조석 조화분해 프로그램에서는 지각 계산 시에 항이 포함되어 있지 않는 로만 이루어진 식 (5)를 사용한다. 이런 관계 측면에서 를 상수로 여길 수 있는 한정된 기간에 식 (9)를 사용하는 것이 더 논리적이다(Bell et al., 1999). 참고로 UTide와 Task2K가 서로 다른 천문변수 계산식(Table A1)을 사용하고 있지만, 두 프로그램으로부터 산출된 와 의 값은 각각 소수점 셋째자리에서 차이가 있을 정도로 그 차이가 작다.
유의할 점으로 조석 조화분해 프로그램 간 이러한 계산식 차이로 인한 사용상 오류를 방지하기 위해 조석 조화상수를 이용한 조위 예측 시에는 동일 package의 조석 조화분해·예측 프로그램을 사용해야 한다(Bell et al., 1999). 예를 들어, Task2K의 ‘tira.f’로 조석 조화분해를 했다면, 이 조화분해 결과를 이용하여 조위를 예측할 경우에 Task2K의 ‘marie.f’를 사용해야 한다.
4.2 분석자료 길이에 따른 Sa 조화상수의 안정도
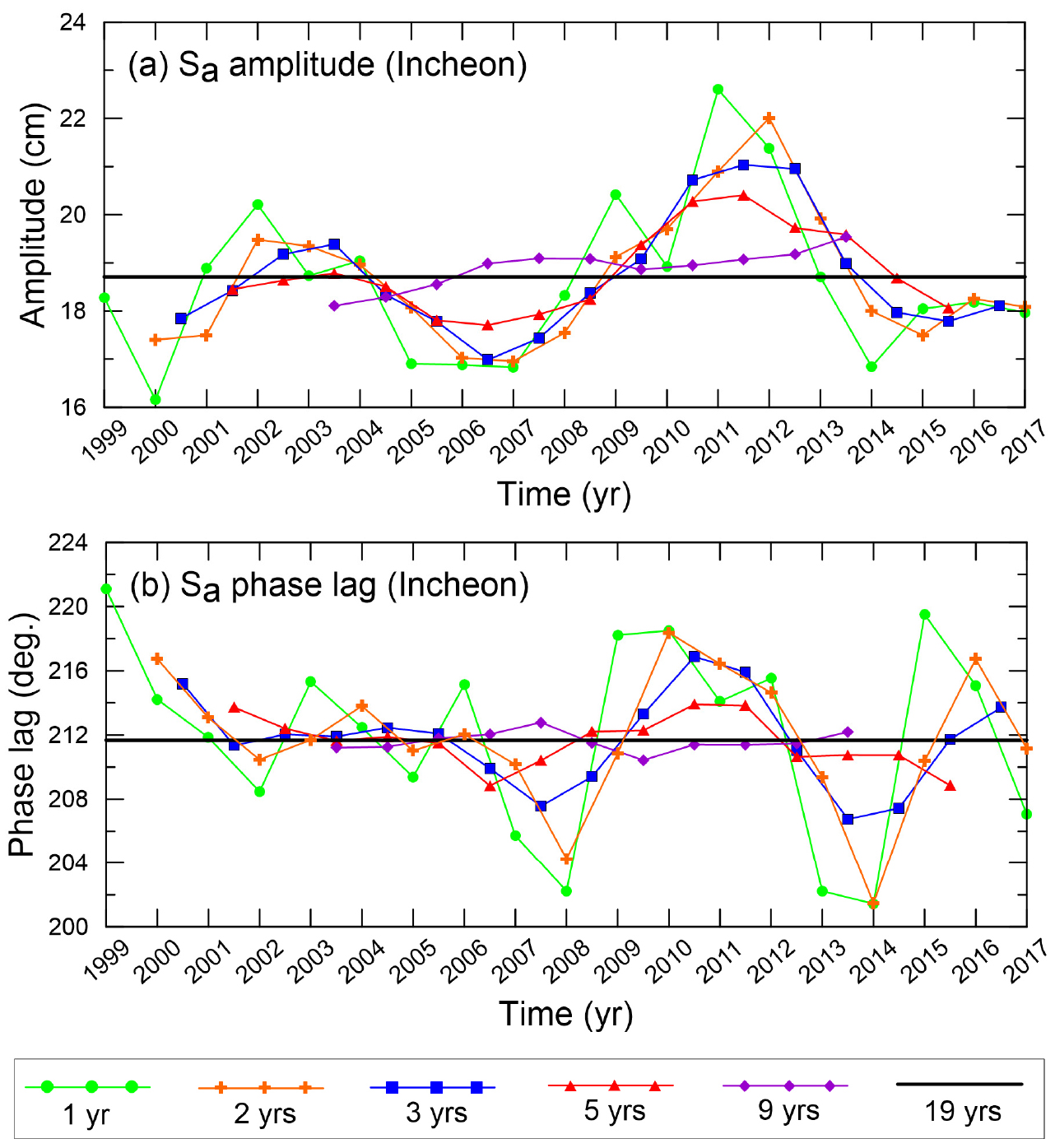
앞 절에서 살펴 본 인천 조위관측소의 19년 해수면 높이 관측자료 분석 결과에서 알 수 있듯이, 1년 해수면 높이 자료의 조화분석 결과는 입력자료 시작 일에 따라 분조의 진폭과 지각의 변화폭이 각각 최대 9.2 cm와 25°이었다. 앞에서 살펴보았듯이 분조는 해수면 자료에 반영된 일사량과 대기압을 포함한 기상 조건(meteorological conditions)과 수온, 염분, 수심 등 수로학적 조건(hydrographic conditions)에 크게 영향을 받기 때문에, 매년 그 진폭과 지각의 변화 폭이 크다. 이로 인해, 인천 조위관측소처럼 분조의 진폭이 다른 분조들의 진폭에 비하여 상대적으로 큰 해역의 경우에 과거 특정 해의 관측자료로 분석된 조화상수로 다른 특정 해의 조위를 예측할 경우에 분조의 변동성 때문에 예측 조위에 분조의 변동성만큼 큰 오차를 발생시킬 수 있다.
이와 관련하여 조위 예측에 사용되는 분조의 불확실도를 줄일 수 있는 방법을 모색하기 위해 조석 조화분해에 사용되는 관측자료 길이(기간)를 달리하여 분조의 조화상수 결과의 변동성을 살펴보았다. 즉, 인천 조위관측소에서 19년 (1999~2017년) 간 관측한 해수면 자료를 사용하여 조화분해 입력자료의 시작 시기를 1999년에서 1년씩 이동시키면서 분석에 사용할 자료의 기간을 1년(369일), 2년, 3년, 5년, 9년, 19년 간격으로 달리한 실험별로 해당 19개, 18개, 17개, 15개, 11개, 1개 자료 세트들을 각각 조석 조화분해하였다. 이 연구에서 이들 조화분해에 사용된 연자료 길이(기간)에 따른 조석 조화분해 실험들은 각각 , , , , , 에 해당한다. 각 해당 실험별(, , , , )로 산출한 의 진폭과 지각에 대한 평균과 표준편차를 구한 후 19년 연속 분석결과()와 비교하여 그 변동성을 조사하였다. 이 실험에서는 19년 이상 장기 연속자료의 조석 조화분해가 가능한 UTide 프로그램을 사용하였다(Byun et al., 2019).
Fig. 5에서 보여주듯이, 전체적으로 분석에 사용되는 관측자료의 길이가 길수록 분조의 진폭과 지각 모두 변동 폭이 줄어들면서 19년 평균값에 더 가까워지는 것을 알 수 있다. 즉, 각 실험별로 산출된 진폭의 평균과 지각의 평균은 각각 18.6~18.9 cm와 211.6~212.0°로 19년 진폭(18.7 cm)과 지각(211.7°)과 비교했을 때, 작은 차이(0.2 cm 이내, 0.3° 이내)를 보인다. 하지만 실험 일 때는 진폭과 지각의 표준편차가 상대적으로 커서 1.7 cm와 6.1°이었으나, 분석자료의 길이가 늘어나면 이들 표준편차는 점차 감소하여 일 때는 진폭과 지각의 표준편차는 0.9 cm와 1.6°로 감소하였다(Table 3). 또한 일 때는 진폭과 지각의 표준편차가 0.4 cm와 0.6°로 줄어들었다.
Table 3.
Stability of Incheon constants derived from harmonic analyses of different length records (1, 2, 3, 5, 9 and 19 years) over the period 1999-2017 using UTide
Table 3에 제시된 관측자료 길이에 따른 조화분해 결과 값(평균값(mean), 최댓값(max), 최솟값(min))을 사용하여 실험별 진폭의 안정도(S)를 다음과 같이 구하였다(Rikiishi and Ichiye, 1986).
가 1이면 안정도가 가장 높고, 1보다 작을수록 안정도가 낮아진다. 실험별 진폭의 표준편차와 마찬가지로 진폭의 안정도는 분석자료의 길이가 늘어남에 따라 커져서 1에 가까운 값으로 수렴한다. 예를 들어, 진폭의 안정도는 일 때 0.78에서, 일 때 0.86으로 향상되었다(Table 3). 이들 결과는 특히 각국의 조석담당 기관에서 조위 예측 시에 실무적으로 장주기 분조들에 대해 수 년 간의 벡터 평균 조화상수를 사용(GLOSS, 2011)하는 이유를 뒷받침한다.
그렇다면, 조석표 제작에 있어서 어떤 방식으로 산출된 조화상수를 사용할 때 조위 정확도 향상 측면에서 더 이점이 있는지 살펴보았다. 현재(Y) 국립해양조사원에서 발간하는 조석표는 1년 전(Y-1)의 관측자료를 이용해서 전년도 예보조화상수로 사용한 M2 지각과의 편차가 2.4°(서·남해안) 또는 4.8°(동해안) 이상일 경우 전년도(Y-1) 관측자료로 산출한 조석 조화상수를 그 다음 해(Y+1)의 예측 조위 생산에 사용하고 있다. 이 경우에, 예컨대 2013년에 2012년 인천 조위관측소의 해수면 높이 자료를 이용한 조위 예측 결과로 2014년의 조석표를 제작한다고 했을 때, 2012년 분조의 진폭과 지각 모두 2014년에 비해 각각 4.5 cm와 13° 더 크다. 이러한 예기치 못한 조화상수의 큰 변동성으로 인한 불확실한 오차를 줄이기 위해 어느 정도 기간의 장기 관측자료로부터 산출된 조화상수를 사용하는 것이 더 좋은지 알아보았다. 이를 위해 해당 실험(, , , , , )별 연별 분석결과를 연별로 이동하면서 의 그 다음 해 분석결과와의 진폭과 지각에 대한 평균제곱근 편차(Root Mean Square Deviation, RMSD)와 벡터 차(vectorial differences)의 평균(VDM)과 표준편차(VDstd)를 구하여 비교하였다.
구체적으로 분조의 진폭과 지각에 대한 RMSD는 각각 다음과 같이 계산하였다. 앞에서 설명한 국립해양조사원의 조석표와 조석표 제작에 사용된 관측자료 간의 시기 차이를 고려하여, 어떤 특정 해에 그 이전 년 동안의 관측자료를 사용해서 다음 해의 분조의 진폭과 지각을 예측했을 때, 발생할 수 있는 예측오차의 표준편차를 계산하였다.
여기서, 은 분석에 사용된 관측자료의 길이(=1, 2, 3, 5, 9, 19년)이다. 당해 연도 이전 년 동안의 관측자료가 있을 때 이 관측자료의 시작연도를 라고하면, 관측자료의 마지막 연도는 이고 당해 연도는 이며, 분조의 진폭과 지각을 예측해야할 다음 해는 이다. 와 는 각각 분조의 진폭과 지각이며, 이들의 아래첨자 와 은 각각 조화분해에 사용된 년도부터 년 동안 관측한 자료와 그 다음 해() 1년 동안의 관측자료를 나타낸다. 는 년도부터 년 동안 관측한 자료를 조화분해해서 얻은 분조의 진폭이고, 는 년도의 1년 동안 관측한 자료를 조화분해해서 얻은 분조의 진폭이다. 국립해양조사원의 조위 예측 체계에 있어서 가 과거 년 동안의 관측자료이고, 는 조위를 예측하는 당해 연도 다음 해 1년에 대한 분조 진폭의 참값이다. 은 분석에 사용된 관측자료 길이(년)별로 에 대응하는 의 총 자료 개수이다.
식 (12)에서 각 실험(, , , , , )별로 실험 과의 벡터 차()에 대한 계산은 보통 조석 수치모델의 분조별 조화상수 검증에 사용되는 다음 식을 사용하였다(Foreman et al., 1993).
유의할 점으로 일 때는 19년 조화상수 값을 일정하게 주어서 과 일대일 대응시켜 RMSD,VDM, VDstd를 계산하였다.
실험 , , , 의 진폭에 대한 각각의 RMSD는 2.30~2.35 cm로 서로 큰 차이가 없었으나, 지각의 경우 각각의 RMSD는 7.02~10.28°로 1년에서 5년까지 사용된 분석자료의 길이가 길수록 이들 값들이 줄어듦을 확인할 수 있다(Fig. 6a, Table A2). 이들 조화상수의 VDM은 2.18~2.61 cm이었으며, 이 중 의 경우에 VDM은 2.21 cm로 보다 0.03 cm 더 컸지만, VDstd는 0.73 cm로 , , 에 비하여 상대적으로 0.44~0.49 cm 더 작은 값을 보였다. 은 에 비해 VDM과 VDstd가 각각 0.16 cm와 0.08 cm로 더 작았다(Fig. 6b, Table A2). 이처럼 4년 더 긴 자료를 사용했음에도 그 향상 정도는 상대적으로 크지 않았다. 이 결과에서 알 수 있듯이 5~9년 동안의 해수면 관측자료를 사용할 경우에 진폭과 지각 예측오차의 표준편차(RMSD)가 각각 2.35 cm와 7.05° 이하로 줄어든다. 19년 해수면 관측자료를 사용할 경우에 진폭과 지각 예측오차의 표준편차(RMSD)가 각각 1.61 cm와 5.89° 정도이다(Fig. 6a, Table A2). 미국 해양대기청(NOAA)의 운용 해양 자료 및 서비스 센터(Center for Operational Oceanographic Products and Services, CO-OPS)에서는 일반적으로 5년 동안 일년씩 조화분해한 결과를 벡터 평균하여 일주조와 반일주조의 조화상수들을 산출하지만, 와 분조의 경우 매년 1년 관측자료를 조화분해한 이들 분조의 조화상수가 거의 일정한 곳을 제외하고 보통 19년 동안 매년 1년 관측자료를 조화분해한 결과들의 벡터 평균한 결과를 사용한다(NOAA, 2009).
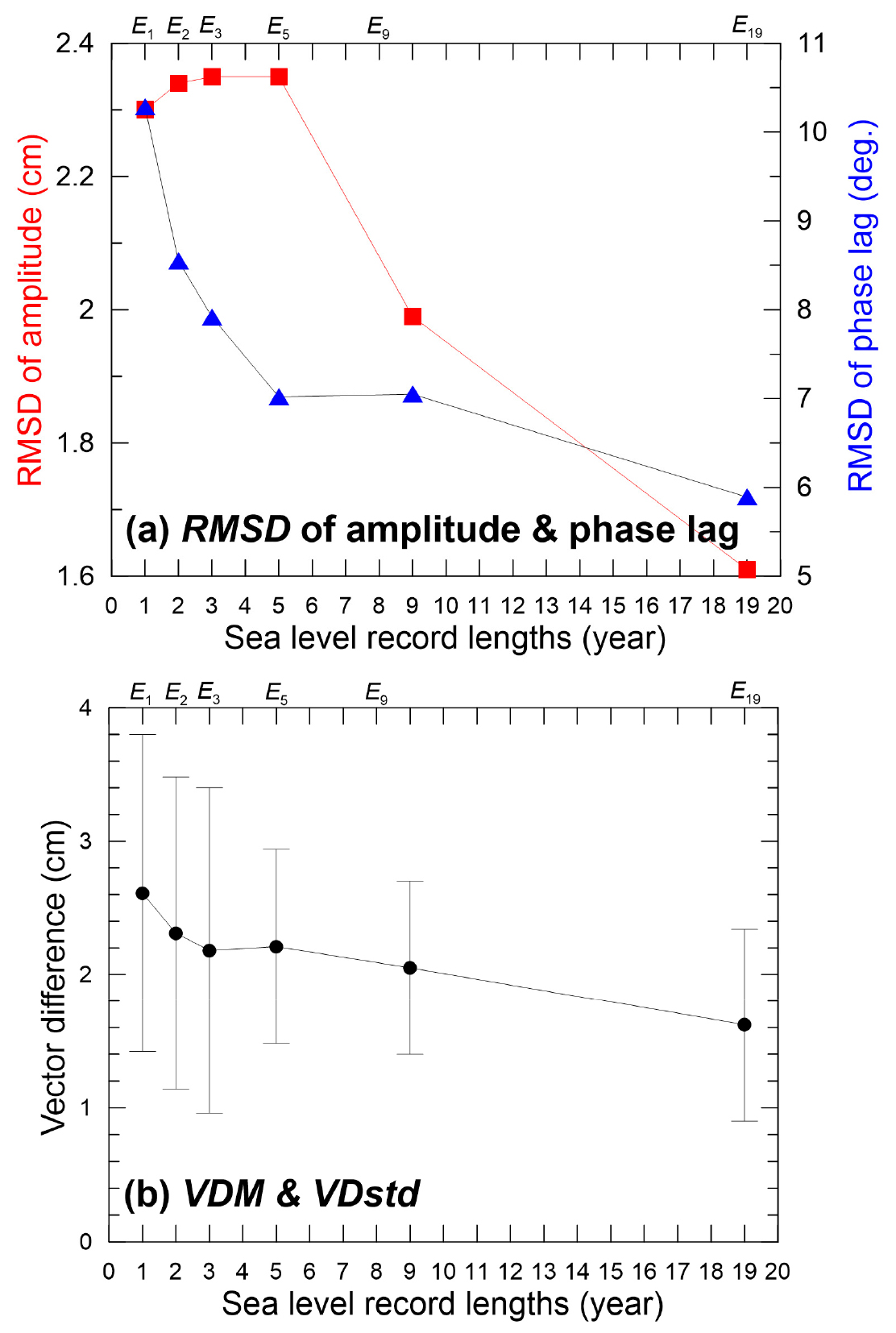
Fig. 6.
(a) Root Mean Square Differences (RMSD) for Incheon amplitudes and phase lags, and (b) mean (VDM) and standard deviation (VDstd) vector differences calculated from the harmonic analysis results produced for each experiment (En) with different sea level record lengths (n=1, 2, 3, 5, 9 and 19 years).
4.3 해역별 Sa 조화상수 분포 특성
우리나라 동·서·남해안에 위치한 21개 조위관측소에서 19년(1999-2017년) 동안 관측한 해수면 높이 자료를 연별로 분석·평균하여 조화상수의 공간적 분포 특성을 살펴보았다(Table 1). UTide를 사용하여 분석한 결과를 중심으로 살펴보면, 진폭은 전 해역에서 10.5~18.6 cm를 분포를 보였으며, 해역별로 서해안에서 15.0~18.6 cm로 가장 컸고, 이어서 제주도를 포함한 남해안에서 10.7~17.5 cm이었으며, 울릉도를 포함한 동해안에서 10.5~13.0 cm로 다른 해역에 비해 상대적으로 작았다. 서해안에 위치한 조위관측소 중에서도 보령과 인천 조위관측소의 진폭이 평균 18.6 cm로 가장 컸다. 반대로 동해안에 위치한 묵호 조위관측소의 진폭은 평균 10.5 cm로 가장 작은 값을 보였다. 전체적으로 진폭에 대한 표준편차의 경우, 가장 큰 값을 보인 울릉도 조위관측소(5.9 cm)를 제외하고 전체적으로 2 cm 내외의 유사한 값을 보였다.
지각의 해역별 분포 특성을 살펴보면, 지각은 서해안에서 212~219°이었고, 남해안에서 221~227°로 가장 남단에 위치한 서귀포 조위관측소에서 가장 큰 값을 보였으며, 이어서 제주 조위관측소와 추자도 조위관측소에서 평균 225°로 큰 값이다. 거문도 조위관측소에서 지각은 224°로 이 두 관측소와 비슷한 값을 보였다. 동해안에서 지각은 가장 큰 값을 보인 울릉도 조위관측소(234°)를 제외하고 217~222°이었다. 동해안 조위관측소 중 가장 위도가 높은 곳에 위치한 속초 조위관측소의 경우, 여름에 주변 해역이 다른 곳보다 저층 수온이 더 낮게 유지되어 지각이 217°로 가장 작았다(Kim and Min, 2008; Lee et al., 2019). 즉, 분조에 의한 해수면 높이는 서해안에서 8월 상순에 가장 높고, 남해안과 울릉도를 제외한 동해안에서는 8월 중순에, 울릉도에서는 8월 하순에 가장 높다. 지각에 대한 표준편차는 서해안에서 5~7°, 제주도를 포함한 남해안에서 6~9°, 동해안에서 9~14°이었다. 울릉도에서 가장 큰 지각의 표준편차(31°)를 보였다. 인천 조위관측소에서 지각이 비교적 작은 이유는 수심이 상대적으로 가장 얕아 태양복사에 의해 해수의 수온이 기온과 함께 8월 초순에 최대가 되기 때문으로 생각된다. 또한 울릉도 조위관측소의 진폭과 지각 모두 표준편차가 가장 큰 이유는 그 해역을 흐르는 동한난류의 주축이 해마다 남북으로 크게 변동할 뿐만 아니라 울릉 난수성 소용돌이의 위치와 규모가 변화하기 때문으로 생각된다(Kim et al., 2002; Choi et al., 2009).
4.4 월평균 해수면, Sa와 Ssa의 합성 조위, 대기압 보정 해수면, 비부피 높이 간 관계
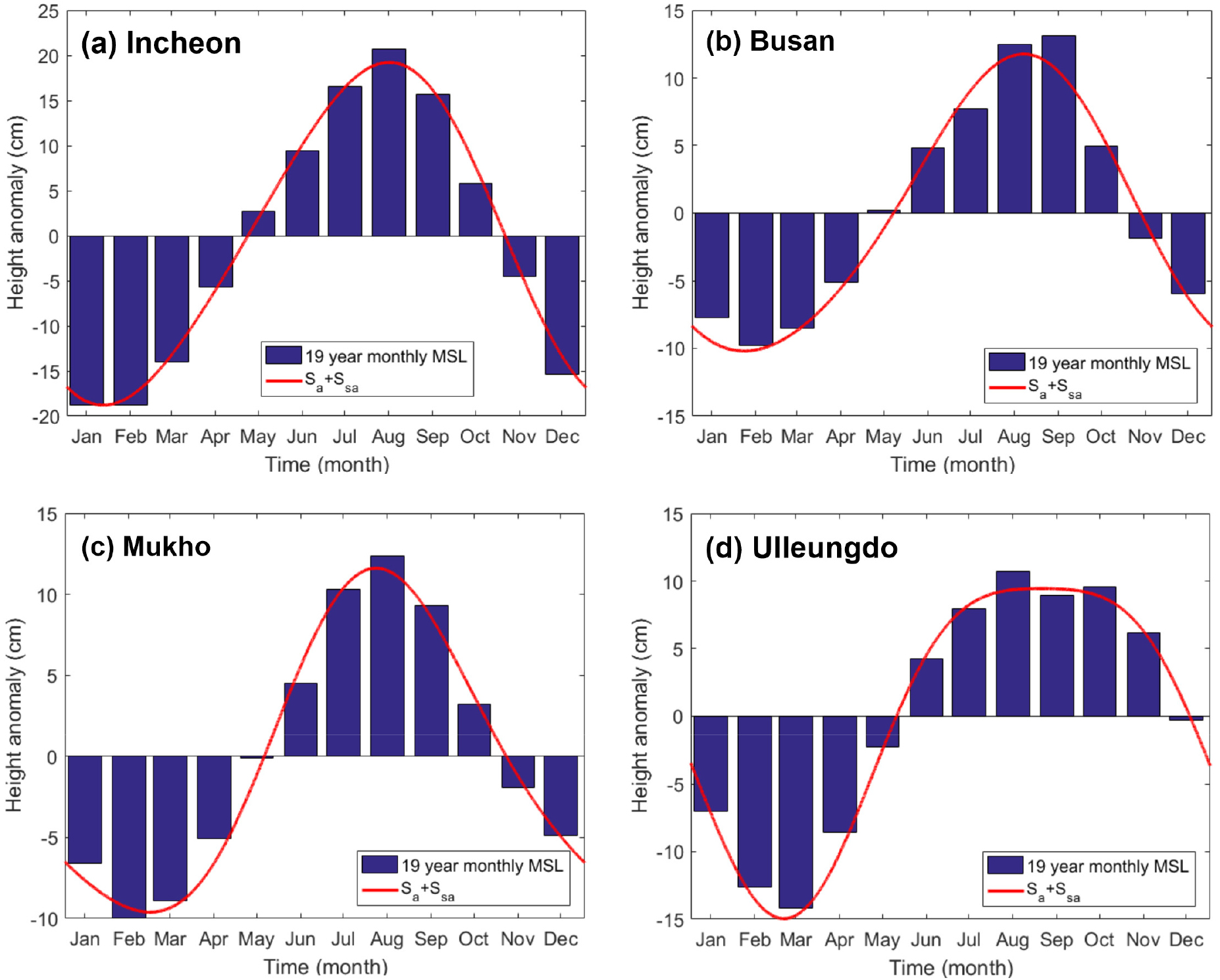
조석 조화분해로 산출된 와 분조의 조화상수만 이용하여 합성한 조위가 평균해수면의 계절변동을 유사하게 표현할 수 있을지 조사하였다. 이를 위해, 4곳 조위관측소(인천, 부산, 묵호, 울릉도)의 19년(1999-2017년) 간 해수면 관측자료로 월평균 해수면자료를 산출하였다. 또한 UTide를 사용하여 동일 기간의 19년 해수면 관측자료를 조화분해하여 산출한 와 분조의 조화상수만을 사용하여 임의의 해(2020년)에 대하여 1년간 조위를 예측하였다. 먼저, 이들 조위관측소의 월평균 해수면의 편차 변화에서 알 수 있듯이(Fig. 7), 우리나라 연안 해역에서 해수면은 겨울철에 낮고 여름철에 높은 뚜렷한 계절변화를 보인다. 월평균 해수면의 편차 값과 와 분조의 합성 조위를 서로 비교하면, 전체적으로 와 분조의 조위 합이 해수면의 계절별 비대칭성을 포함(Appendix A4)하여 월별 평균해수면 변동을 잘 반영하고 있다(Fig. 7). 특히, 울릉도 조위관측소의 경우, 분조에 의한 조위의 비대칭 효과(Fig. A2c)에 의해 7월부터 10월까지 월별 해수면 높이 편차가 거의 비슷한 특성을 잘 보여준다.
이어서 해역별 월평균 해수면 변동 즉, 와 합성 조위의 연변동에 영향을 미치는 주요 요인이 무엇인지 조사하였다. 해수면은 크게 해수의 밀도 변화와 관련된 비부피 효과(steric effect)와 외력(기압, 바람 등)과 역학작용에 의한 효과(non-steric effect)에 의해 변한다. 먼저, 비부피 높이(steric height)를 계산하여 해수 밀도 변화가 해수면의 계절변화에 어느 정도 기여하는지 정량적으로 추산하여, 월평균 해수면 변동과 조위 변동과의 관계를 살펴보았다.
이들 조위관측소에서 가장 가까운 곳에 위치한 국립수산과학원 정선해양관측 정점의 연직 수온·염분(CTD) 관측자료(1999-2017년)를 사용하여 다음 계산식으로부터 비부피 높이()를 계산하였다.
여기서, 는 중력가속도, 는 기준 압력, 는 해수의 밀도, 는 비부피(specific volume)이다. 기준 압력으로 연안 조위관측소의 경우 얕은 수심을 고려하여 30 dbar로 설정하였고, 울릉도의 경우는 300 dbar로 설정하였다. 국립수산과학원 정선해양관측 정점 중에서 연안 조위관측소(인천, 부산, 묵호)와 가장 가까우면서 수심이 30 m보다 깊은 곳(307-03, 207-01, 105-03)을 선정하여, 해표면에서부터 30 m까지의 수온과 염분 자료(2, 4, 6, 8, 10, 12월)를 이용하여 비부피 높이를 계산하였다. 해수면 아래 30 dbar보다 더 깊은 곳에서 해수의 밀도변화가 일어나서 비부피 높이에 영향을 줄 수 있으나, 그 영향이 상대적으로 작다고 가정하였다. 울릉도의 경우는 울릉도 조위관측소와 가장 가까우면서 결측이 최소이고 수심 300 m보다 깊은 곳(105-10)을 선정하여, 동일하게 해표면에서부터 300 m까지의 수온과 염분자료(2, 4, 6, 8, 10, 12월)를 이용하여 비부피 높이를 계산하였다. 월평균 해수면 편차와 비교하기 위해 계산한 비부피 높이 값에서 평균값을 빼주어 비부피 높이 편차를 구하였다.
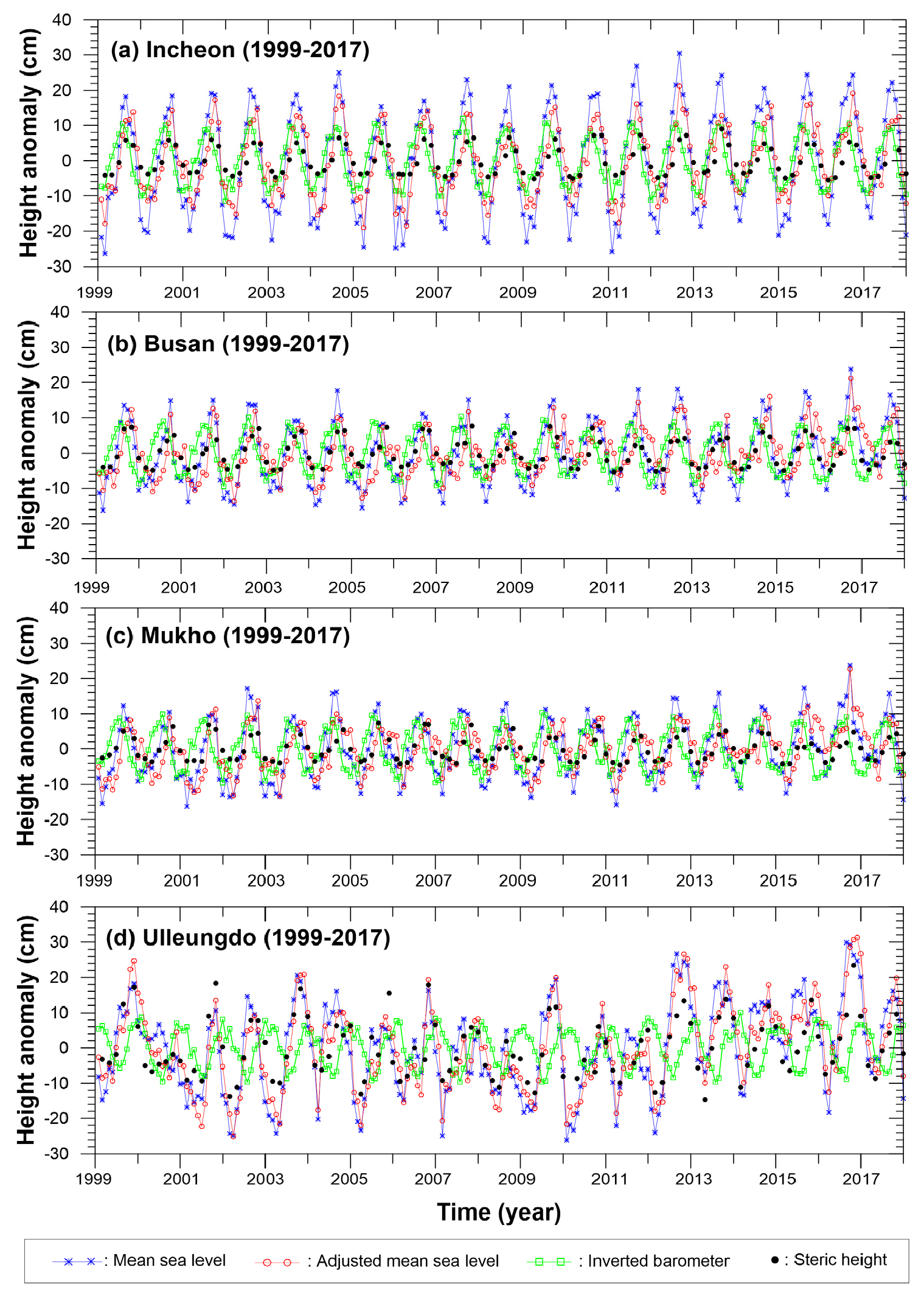
월평균 해수면은 8~9월에 가장 높고, 2~3월에 가장 낮다(Fig. 8에서 *를 가진 파란 실선). 이러한 해수면의 계절 변화는 대기압, 해수 밀도의 계절 변화 때문에 일어난다(Fig. 8). 또한 바람, 강물유입 그리고 해류의 계절 변화도 영향을 미칠 수 있다. 월평균 대기압을 정수압 방정식(hydrostatic equation)으로 변환한 역기압 해수면(inverted barometer sea level) 편차는 7월에 가장 높고, 1월에 가장 낮아 계절적으로 대칭적인 모습을 보인다(Fig. 8에서 □를 가진 연두색 실선). 또한 해수 밀도 변화에 따른 해수면 편차는 지점마다 최댓값과 최솟값이 나타나는 달이 다르다(Fig. 8에서 빨간색 ●). 이처럼 해수 밀도 변화의 위상과 진폭이 해역마다 달라서 월평균 해수면의 진폭이 해역마다 다르고 그 계절적 변화도 비대칭적이다. 해수면에서 대기압변화에 의한 해수면 변화를 제거하고 구한 월평균 해수면 변화(air-pressure adjusted mean sea level; 기압보정 월평균 해수면)는 거의 해수 밀도 변화에 의한 월평균 해수면 변화와 비슷하다. 기압보정 월평균 해수면의 계절 변화가 비부피 해수면 편차의 계절 변화와 차이가 나는 이유는 비부피 해수면 편차를 계산할 때 사용되는 기준 압력면의 불확실성과 함께 시·공간적으로 수온·염분 관측 자료가 부족하고, 바람에 의한 해수면 변화가 기압보정 월평균 해수면에는 포함되어 있기 때문이다. 특히, 인천 조위관측소의 경우(Fig. 8a)에는 기압보정 월평균 해수면 편차와 비부피 해수면 편차의 계절 변화의 위상은 일치하지만, 비부피 해수면이 상대적으로 겨울철에 높고 여름철에 낮아 이로 인해 이들 간 진폭에는 큰 차이가 있다. 여름철(겨울철)에 기압보정 월평균 해수면 편차가 비부피 해수면 편차보다 높은(낮은) 것은 Kang et al.(2008)이 해양수치모델을 이용하여 구한 바람에 의한 해수면의 계절변화 결과와 일치한다.
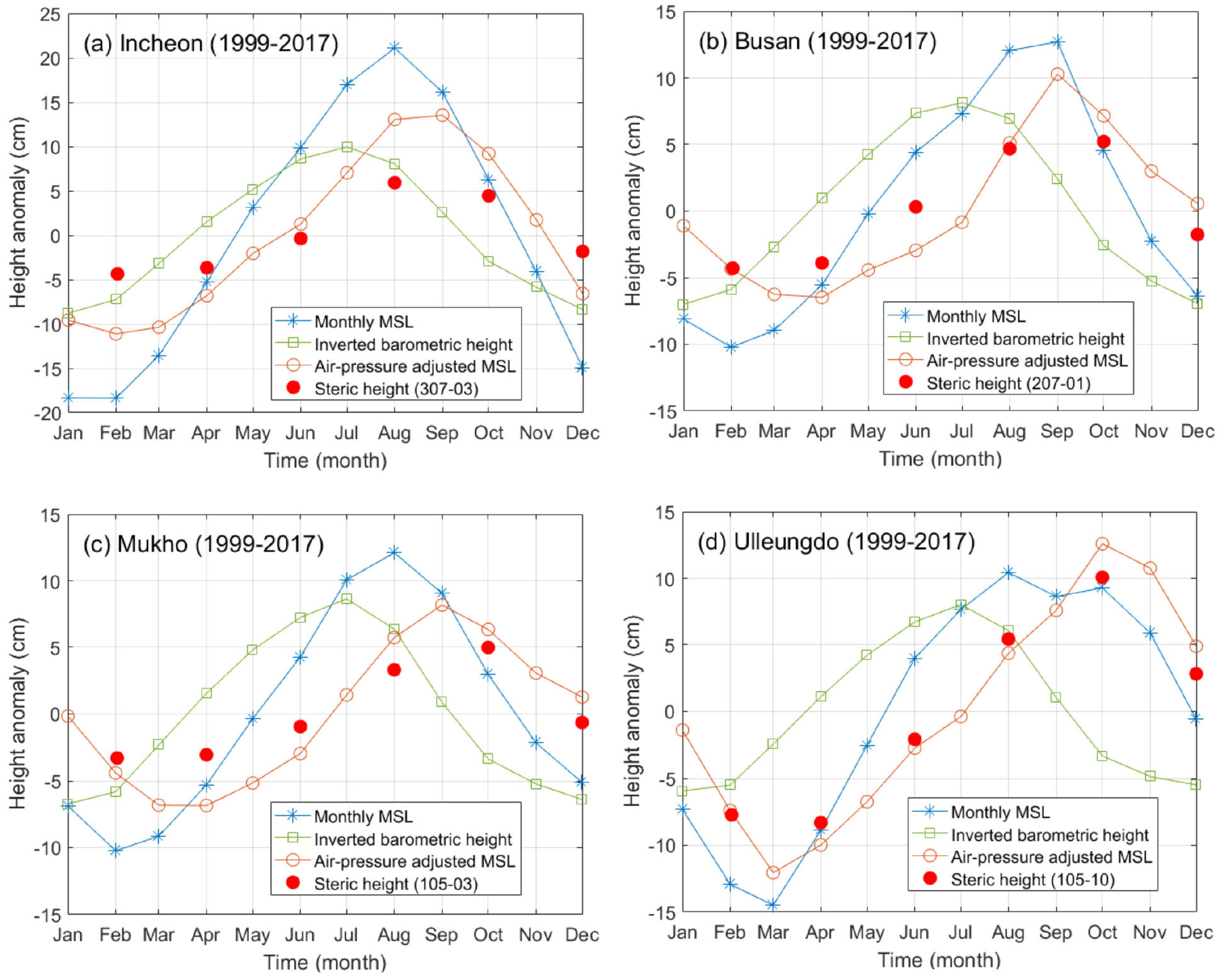
Fig. 8.
Comparisons between 19-year-averaged monthly data on the mean sea level (MSL) anomaly, air pressure derived inverted barometric height, air pressure adjusted MSL anomaly (MSL anomaly + air pressure anomaly) and steric height anomaly, calculated from the 1999 to 2017 sea-level records of (a) Incheon, (b) Busan, (c) Mukho, and (d) Ulleungdo Tidal Stations, plus CTD and air-pressure records observed near each tidal station, provided by the National Institute of Fisheries Science and the Korea Meteorological Administration.
월평균 해수면의 계절 변화가 비대칭성을 갖는 주된 이유는 비부피 해수면의 계절 변화가 비대칭이기 때문이다. 조화분해 방법에선 월평균 해수면의 연변화 비대칭성을 와 분조의 합으로 표현하지만, 실제 월평균 해수면 변화는 크게 월별 역기압 해수면과 월별 비부피 해수면 간 위상이 달라서 나타나며, 또한 비부피 해수면의 변화가 계절적으로 비대칭이기 때문이다. 추가로 Fig. 9에서 보여준 대기압 효과가 실제 와 분조에 정량적으로 어느 정도 영향을 미치는지 알아보았다. 이를 위해 4곳의 동일한 조위관측소를 대상으로 1시간 간격의 해수면 높이 관측 값(STH)에서 이에 해당하는 기압편차 값(APH)을 빼주어 기압 효과를 보정한(ATH) 후 해수면 높이 관측 자료를 조석 조화분해하여 보정 전후 와 조화상수 차이를 비교하였다. 대기압 보정 후에 인천, 부산, 묵호 조위관측소의 경우 의 진폭 감소율이 각각 40.3%, 36.9%, 35.5%로 큰 폭으로 감소하였다. 그러나 울릉도 조위관측소의 진폭 감소율은 8.4%로 상대적으로 작았다(Table 4). 울릉도 대기압의 진폭이 7.2 cm임에도 불구하고, 이 결과는 Fig. 8d에서 보여 준 울릉도 조위관측소의 해수면 변화가 해수 밀도 변화에 따른 해수면 변화에 더 지배적으로 영향을 받고 있음을 뒷받침한다. 한편, 2.5 cm 미만의 진폭 값을 갖는 의 경우, 대기압 보정 후에 인천과 부산 조위관측소에서 7.1~10.5% 진폭이 상승한 반면에 묵호 조위관측소에서 진폭이 44.4%로 큰 폭으로 감소하였고 울릉도 조위관측소에서 진폭이 4.3% 소폭 감소하였다. 지각의 경우, 대기압 보정 후 4곳의 조위관측소에서 26~49° 만큼 더 커졌다. 그러나 지각의 경우, 인천, 부산, 묵호 조위관측소에서 21~52° 만큼 더 커졌으나 울릉도 조위관측소에서는 50° 감소하였다. 이러한 대기압 보정에 의해 와 간의 진폭 비는 인천, 부산, 울릉도 조위관측소에서 각각 85.8%, 69.8%, 4.5% 증가하였으나 묵호 조위관측소에서는 13.7% 감소하였다(Table 4). 이 결과로부터 인천과 부산 조위관측소의 월평균 해수면의 연변화 비대칭 정도는 대기압 효과에 의해 크게 완화되는 반면에 울릉도 조위관측소에서는 이 효과에 의해 조금 완화되고, 묵호 조위관측소에서는 오히려 약간 강화됨을 알 수 있다.
Table 4.
Comparison of harmonic analysis results for the and constants derived using UTide and hourly-interval 19-year records (1999-2017) of air-pressure (APH), original sea level (STH) and air-pressure adjusted sea-level (ATH) from four tidal stations
Fig. 5a에서처럼 인천 조위관측소에서 1~3년 해수면 높이 자료로 구한 진폭이 수년 주기로 크게 변화되는 주된 이유는 대기압과 바람이 수년 주기로 천천히 변화하기 때문이다(Han et al., 2020). 이와 관련하여 1999년부터 2017년까지 해마다 월평균 해수면 편차, 비부피 해수면 편차, 역기압 해수면 편차를 계산하여 이들 조위관측소에서 각 해의 월평균 해수면 변동에 영향을 미치는 대기압과 해수 밀도 변화 효과를 알아보았다. 인천 조위관측소의 경우 전반적으로 비부피 해수면 편차와 월평균 역기압 해수면 편차가 해마다 크게 변화하지 않는다. 예를 들어, Fig. 9a에서 2005년과 2011년을 비교하였을 때 월별 역기압 효과에 의한 해수면 편차와 비부피 해수면 편차 모두 두 해에 서로 비슷하지만, 기압보정 월평균 해수면 편차의 경우 2005년에 비해 2011년에 더 큰 편차를 보여 결국 기압보정 월평균 해수면 편차가 두 해의 월평균 해수면 편차 간 큰 차이를 이끈다. 이러한 차이는 겨울철에 북풍 계열의 풍속과 여름철에 남풍 계열의 풍속 간 차이와 강물 유입량의 차이와 관련이 있을 것으로 생각되며, 향후 이를 뒷받침할 추가 연구가 필요하다. 울릉도 해수면 높이의 경우는 비부피 해수면이 해마다 크게 변하여 해수면의 계절변화 진폭도 해마다 크게 변화한다(Fig. 9d). 울릉도 주변 해역의 비부피 해수면은 동해 극전선의 위치에 따라 크게 변화하는 것으로 알려져 있다(Kim et al., 2002; Choi et al., 2009).
5. 결 론
태양 연주조 와 태양 반년주조 는 비천문조로 계절적 해양·대기 영향에 의한 매년 다른 해수면의 계절변동 시그널을 담고 있다. 우리나라 연안역에 위치한 21개 조위관측소에서 19년(1999-2017년) 동안 장기 관측한 해수면 높이 자료를 사용하여 분석자료의 시작 시기와 길이에 따른 조화상수의 변동성을 조사하였다. 이를 위해 먼저, Task2K (Bell et al., 1999)와 UTide (Codiga, 2011) 조화분해 프로그램으로부터 산출된 조화상수를 비교하였으며, Task2K의 지각 값이 UTide에 비해 약 78°정도 더 작은 이유가 지각 계산 시에 20,942년 주기를 갖는 근일점 천문변수 (perihelion)를 Task2K에서는 고려하지 않기 때문이라는 사실을 알 수 있었다. 이처럼 조석 조화분해 프로그램마다 관련 계산식이 다르기 때문에 이 점을 고려하여 조위 예측에 있어서 조화분해 프로그램과 동일한 계열의 조석 예측 프로그램을 사용해야 한다. 예를 들어, UTide, IOS (Foreman, 1977), T_Tide (Pawlowicz et al., 2002)는 근본적으로 분조의 주기와 계산식이 같은 동일 계열의 조석 조화분해 프로그램이므로, 이들 프로그램으로 산출된 조화분해 결과를 사용하여 이들 중 어느 한 조석 예측 프로그램으로 조위를 정확하게 예측할 수 있다. 또한 이러한 조석 예측 프로그램 사용 상 오류를 없애기 위해 분석 결과 작성 시에 사용한 조석 조화분해 프로그램 이름을 명기하는 것이 바람직하다.
만약 1년간 해수면 높이를 관측해서 다음 해의 조위 예측을 위한 조화상수를 구할 경우, 조화분해에 사용된 관측자료의 시작 일에 따라 산출되는 조화상수는 크게 달라질 수 있다. 이는 대기압과 해수밀도 변화가 시간에 따라 불규칙하게 크게 일어나기 때문이다. 인천 조석관측소의 경우 20년(1999-2018년)간 자료를 하루씩 이동하면서 1년(369일) 자료를 조화분해한 결과 1년 관측 시기에 따라 발생하는 진폭과 지각의 변화 폭은 각각 9.2 cm와 24.5°이었다.
조화상수의 큰 해해변화로 인한 특정 해의 조화상수로 임의의 해에 대한 조위 예측 정확도의 불확실도를 줄이기 위해 분석에 사용된 자료 길이에 따라 산출된 조화상수들의 변동성과 안정도를 조사하였다. 그 결과 5~9년 동안의 관측자료를 조화분석에 사용하였을 때 다음 해 1년에 대한 조화상수 예측오차가 상당히 줄어들었으며, 가능하다면 19년 관측자료를 사용하는 것이 바람직하다는 결론을 얻었다. 더 나아가, 의 진폭이 주요 4대 분조에 속할 정도로 상대적으로 큰 해역에서는 수심과 해안선의 기준이 되는 약최저저조면과 약최고고조면 계산 시에 이 분조의 효과를 적절히 고려가 필요가 있다. 이 경우, 안정적인 조석 조화상수 값을 얻기 위해서는 19년 조화분해 결과를 사용하는 것이 바람직하며, 적어도 9년 이상의 해수면 높이 자료를 사용하면 변동성을 크게 줄일 수 있다. 인천 조위관측소 해수면의 조화상수가 큰 해해변화를 갖는 가능성 있는 이유 중 하나로 매년 크게 변하는 바람에 의한 해수면 상승과 하강을 들 수 있다. 따라서 이와 관련한 보다 심도있는 추가 연구가 요구된다.
우리나라 동·서·남해안의 조화상수 값의 분포 특성 파악을 통해 조화상수가 이들 해역의 해양·대기 물리학적 특성을 반영하고 있음을 알 수 있었다. 또한 우리나라 해역에서 진폭이 상대적으로 작음에도 불구하고 분조에 더해졌을 때 해수면의 연변화에 비대칭성을 만들고, 분조로 인해 해수면의 연변화에서 연중 최고(최저) 해수면 높이 발생 시기가 늦어지거나 빨라질 수 있음을 보여주었다. 이러한 월평균 해수면의 연변화 비대칭성은 주로 월별 해수 밀도 변화가 계절적 비대칭성을 갖고 있어서 발생한다.
Appendix
A1. UTide와 Task2K 프로그램에서 사용되고 있는 주요 천문 변수식
Table A1.
Formulas for major astronomical variables used in UTide and Task2K tidal packages
| Astronomical variables (period) | Angular speed (° hr-1) | UTide (Codiga, 2011) | Task2K (Bell et al., 1999) |
|
1200 UT Dec. 31, 1899 for time origin (i.e., T=0) |
0000 UT Jan. 1, 1900 for time origin (i.e., Y=1900, D=1) | ||
| T: Mean lunar day (1.03505 msd) | 14.49205212 | - | - |
| s: Sidereal month (27.32158 msd) |
0.5490165207 | s=270.434164+13.1763965268T -0.000085T-8+0.000000039T-12 | s=277.0247+129.38481 IY +13.17639 DL |
| h: Tropical year (365.242199 msd) |
0.0410686393 | h=279.696678+0.9856473354T +0.00002267T-8 | h=280.1895-0.23872 IY +0.98565 DL |
| p: Moon’s perigee (8.847 years) |
0.00464396 | p=334.329556+0.1114040803T -0.0007739T-8-0.00000026T-12 | p=334.3853+40.66249 IY +0.11140 DL |
| N: Moon’s ascending node (18.613 years) |
0.0022064 | N=259.183275-0.0529539222T +0.0001557T-8+0.00000005T-12 | N=259.1568- 19.32818 IY -0.05295 DL |
| : Perihelion (20,942 years) |
0.0000019617 | =281.220844+0.0000470684T +0.0000339T-8+0.00000007T-12 | =281.2209 + 0.17192 IY |
|
Here, T=τ-τ0 and τ0=693961.5 |
Here, IY=Y-1900 DL=-[INT(IY/4)]+D-1 (for 1801-1899) and DL=-[INT(IY-1/4)]+D-1 (for 1900-2099) |
A2. 계산 방법에 따른 Sa 조화상수 산출 결과 비교
UTide (ut_solve.m)는 조석 조화상수 해를 구할 때 사용하는 ‘반복적 가중의 최소자승법(IRLS)’에 ‘코시 가중함수(Cauchy weight function)’가 기본 함수로 지정되어 사용되고 있으며, ‘Andrews’, ‘Bisquare’, ‘Fair’, ‘Huber’, ‘Logistic’, ‘Talwar’, ‘Welsch’ 함수들 중 하나를 선택할 수 있다. 또한 IOS tidal packages (Foreman, 1977; Foreman et al., 2009)와 T_TIDE (Pawlowicz et al., 2002) 등 전통적인 조석 조화분해 프로그램에서 사용되는 ‘최소자승법(ordinary least squares method, OLS)’도 선택할 수 있다(Codiga, 2011).
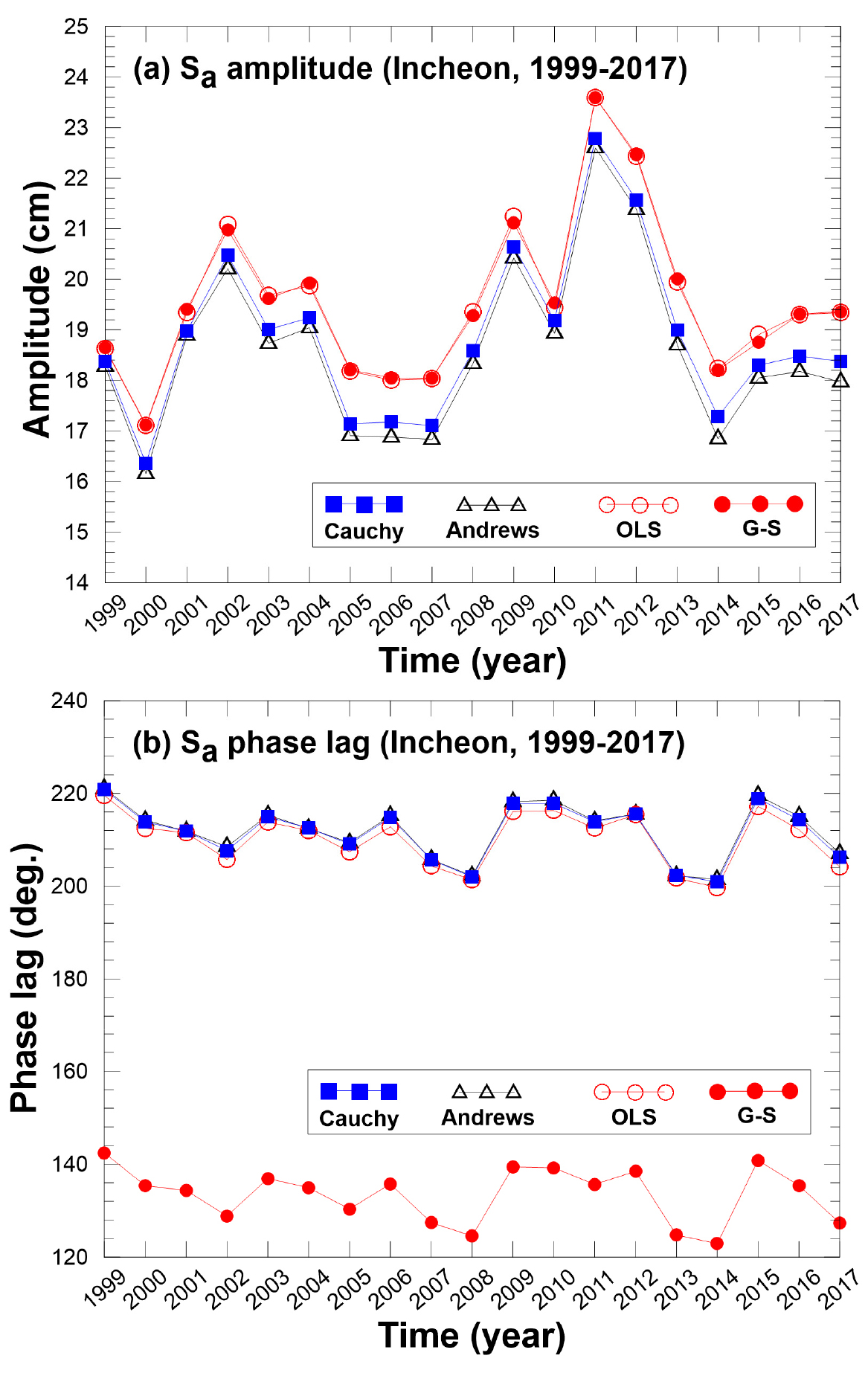
인천 조위관측소에서 19년간(1999-2018년) 관측한 해수면 높이 자료를 사용하여, 견고한(robust) 해를 구하는 방법으로 알려진 IRLS 방법(‘Cauchy’, ‘Andrews’)과 전통적으로 조석 조화분해에 사용되어 온 선형 방정식의 해를 구하는 OLS 방법과 가우스-자아델(G-S) 방법(Task2K의 ‘tira.f’)에 따라 분조에 대한 조화분해 결과가 실제 서로 어느 정도 차이가 나는지 알아보았다. Fig. A1a에서 보여주듯이, IRLS 방법에 Cauchy와 Andrews 가중함수를 사용하여 산출한 진폭들의 19년 평균±표준편차는 각각 18.843±1.624 cm와 18.597±1.652 cm로 이들 진폭 차이는 평균적으로 대략 0.246 cm로 Cauchy가 약간 더 크게 산출되는 경향이 있다. 반면에 선형 방정식의 해를 구하는 OLS와 G-S 방법으로 산출된 진폭들의 19년 평균±표준편차는 각각 19.563±1.596 cm와 19.558±1.588 cm로 이들 평균 진폭 차이는 0.005 cm로 거의 차이가 없다. 이와 같이 OLS(G-S) 방법이 IRLS 방법보다 대략 1 cm 정도 더 크게 진폭이 산출된 이유는 UTide(ut_solve.m)에서 사용하는 IRLS 방법은 극단치(outlier)의 영향을 크게 받지 않는 견고한(robust) 방법이기 때문이다(Leffler and Jay, 2009).
또한 지각의 경우, UTide 프로그램에서 IRLS 방법에 Cauchy와 Andrews 함수를 사용하여 산출된 지각의 19년 평균±표준편차는 각각으로 211.6±6.0°와 212.0±6.0°로 약 0.4° 차이를 보였으며, UTide 프로그램 OLS 방법으로 구한 값은 210.3°±5.9°로 IRLS 방법으로 구한 값보다 평균적으로 약 1° 이상 작게 산출되었다. 그러나 Task2K 프로그램의 G-S 방법으로 산출한 지각의 19년 평균±표준편차는 133.4±5.9°로 UTide 프로그램의 OLS 방법보다 평균적으로 약 77° 작게 산출되었다(Fig. A1b).
A3. 분석자료 길이에 따른 Sa 조화상수의 안정도 실험 결과
Table A2.
Comparisons of Root Mean Square Differences (RMSD) for Incheon amplitudes and phase lags, and mean (VDM) and standard deviation (VDstd) vector differences calculated from the harmonic analysis results produced for each experiment (En) with different record lengths (n=1, 2, 3, 5, 9 and 19 years). Note that N denotes the total number of constants used in calculation
A4. Sa 분조에 의한 해수면 연변화 비대칭 효과
우리나라 연안에서 진폭은 0.6~2.4 cm로 진폭의 10% 내외로 크지 않지만(Table 1), 해수면의 연변화가 비대칭 모양을 갖는 데 영향을 주는 분조이다. 해수면의 연변화 비대칭 정도는 천해 분조가 발달한 연안에서 조위의 비대칭 정도를 나타내기 위해 사용되는 와 분조 간 조화상수 관계식과 유사한 방법(Friedrichs and Aubrey, 1988)으로 와 분조 간 진폭 비()와 상대 지각 차()를 계산하여 알아보았다. 편의 상, 이들 관계식 계산을 위해 와 분조의 조화상수는 정확하게 각속도의 절반인 식 (9)를 바탕으로 한 Task2K 조화분해 프로그램(‘tira.f’)으로 산출된 결과를 사용하였다.
의 값이 클수록, 조위 연변화의 비대칭 정도는 커진다. 해역별 분포는 서해역에서 상대적으로 가장 낮은 0.036~0.124 값을 보이고, 남해역에서 0.096~0.146 값을, 동해역에서 상대적으로 가장 큰 0.125~0.193 값을 보인다(Table 1). 이 중 위도 조위관측소와 울릉도 조위관측소에서 각각 가장 작은 값(0.036)과 가장 큰 값(0.193)을 가진다.
의 값이 어느 정도 클 때, 의 값은 연변화 조위의 비대칭 모양을 결정한다. 가 25.0°인 속초 조위관측소의 경우처럼, 일 때 이들 지각 차에 의해 연중 조위가 가장 낮게 나타나는 시기는 늦추어지고, 조위가 가장 높게 나타나는 시기는 며칠 앞당겨진다. 와 분조 간 조위의 위상이 반대에 가까울 때 이들 합성 조위의 최솟값은 조위에 비해 줄어든 반면에, 최댓값은 이들 조위의 위상 간에 큰 차이가 없어서 합성 조위의 최댓값은 오히려 커진다(Fig. A2a). 이와 반대로, 가 328.0°인 부산 조위관측소의 경우처럼, 일 때, 이들 합성 조위의 특성은 조위에 비해 연중 해수면 높이가 가장 낮게 나타나는 시기는 빨라지고 가장 높게 나타나는 시기는 늦어진다. 또한 이들 합성 조위의 최솟값은 덜 내려가고 최댓값은 더 올라간다(Fig. A2b).
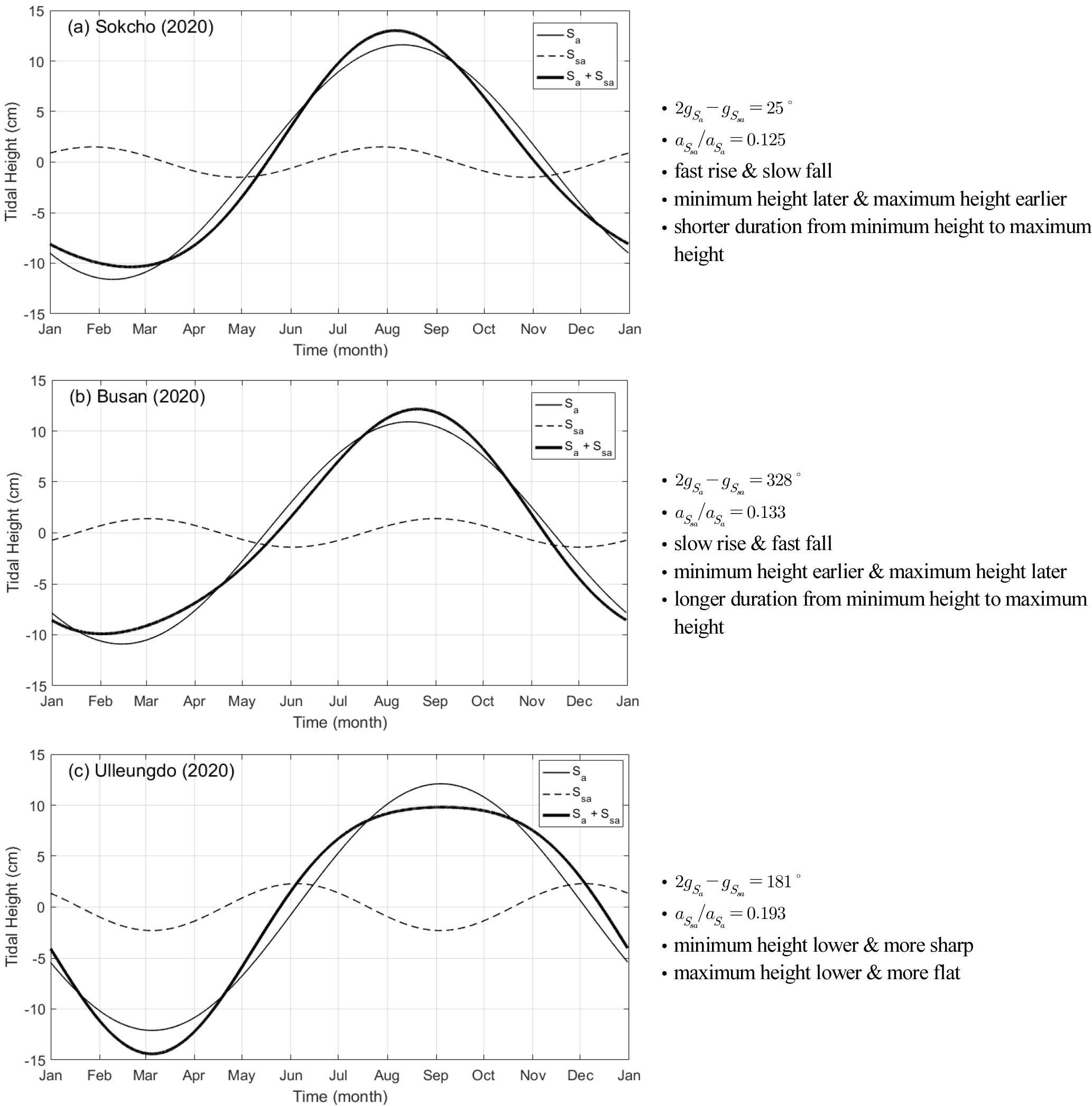
Fig. A2.
2020 sea-level variations predicted from the and constants at (a) Sokcho, (b) Busan, and (c) Ulleungdo Tidal Stations, as listed in Table 1.
해역별로 이러한 상대 지각 차이의 분포를 살펴보면, 서해안에서 276.4~317.9°, 남해안에서 295.8~328.0°, 동해안에서 25.0~344.0°를 보인다. 동해안 북쪽에 위치하여 여름에 저층 수온이 낮게 계속 유지되는 묵호와 속초 조위관측소에서만 상대 지각 차가 에 속한다. 이처럼 동해 일부 해역을 제외하고 우리나라 연안에서 는 대체로 에 속해 분조의 영향으로 연중 최고(최저) 해수면 높이가 발생하는 시기가 늦어(빨라)지는 비대칭적 해수면 변화를 보인다. 한편, 울릉도 조위관측소는 특이하게 상대 지각 차가 181°로 와 조위의 위상이 거의 동일하거나 반대이다. 이로 인해 최저 조위는 더욱 내려가고, 최고 조위는 오히려 내려가는 연변동 특성을 보인다(Fig. A2c).
이들 결과는 값이 0.1 이상으로 클 경우, 분조는 해수면의 연변화 비대칭에 크게 영향을 미칠 수 있음을 보여준다.