1. 서 론
2. 자료 및 방법
2.1 자료
2.2 방법
3. 결 과
3.1 학습 검증 결과
3.2 품질처리 검증 결과
3.3 학습기간 외 기간(2018, 2019)에의 적용
4. 토 의
4.1 과적합 및 과소적합 문제
4.2 Time step 선정 문제
4.3 일반적인 품질처리, 이상치 모니터링 방법과의 비교
4.4 이상값 탐지 모델 개선방향
5. 요약 및 결론
1. 서 론
대한민국의 조위관측소 해수위 자료는 국립해양조사원이 관리하는 바다누리 해양정보 서비스를 통해 국민에게 공개되고 있으며, 총 54개 관측소(조위관측소 48개소, 해양관측소 3개소, 해양관측기지 3개소)에서 상시 관측되고 있다. 실시간으로 공개되는 해수위 자료는 1분 간격의 시간해상도를 가지며, 품질처리(Quality control; QC)가 수행된 조위 통계자료는 익월 15일 이후에 1시간 간격의 시간해상도로 공개된다(KHOA, 2021). 위와 같은 이유로 해양관측 자료 이용자가 높은 시간해상도의 실시간 자료를 사용하고자 할 경우 자체적인 품질처리를 수행해야하는 불편함이 있으며, 품질처리된 자료를 사용하고자 할 경우 차후 공개되는 낮은 해상도의 자료를 사용해야한다.
해양 관측자료 뿐만 아니라 대부분의 관측자료들은 결측값과 오측값을 포함하고 있다. 그 중 오측값은 이상값(abnormal value, outlier)로 분류되는 전처리 대상이며, 많은 과학자와 실무자들은 이 이상값을 처리하기 위해 다양한 방법론을 제시해왔다. 통용되는 이상값은 3σ (three standard deviations) 규칙으로 널리 알려진 경험적 규칙(empirical rule)이 적용되는데, 중앙값(또는 평균값)에서 절대편차의 3배를 초과하여 떨어져 있는 값을 의미한다. 하지만 이 방법은 조위 관측 자료에 일괄적으로 적용하기에는 무리가 있다. 첫 번째로, 기상이변 혹은 재해로 관측되는 극 값의 출현은 이벤트성 자료이므로 정상적인 관측값임에도 불구하고 3σ 규칙에 의해 이상값으로 판별될 수 있다. 두 번째로, 정상 자료 범주내에서 나타나는 이상값(e.g., 지속적인 동일값, 튐 값)은 오측임에도 불구하고 해당 규칙에 의해 제거되지 않을 수 있다. 위와 같은 이유들로 본 연구에서는 조위자료 및 기상자료 품질처리에 적합한 방법을 설계하고자 한다.
본 연구에서 적용하고자 하는 인공신경망(Artificial neural network; ANN)은 기계학습의 한 갈래이다. 기계학습은 근래에 학술분야를 막론하고 각광받는 방법론이며, 데이터 품질처리 분야에서도 예외는 아니다. Omar et al.(2013)은 이상값 탐지를 위한 다양한 지도학습(supervised learning) 및 비지도학습(unsupervised learning) 기법들을 소개하였으며, 각 기법의 적용성 및 장단점을 구체적으로 언급하였다. Goyal et al.(2018)와 Saini and Preeti(2015)는 기계학습 알고리즘이 정해진 규칙(strictly static program instruction)을 따르는 대신 입력된 데이터로부터 모델을 구축한다는 것을 언급한 바 있다.
기존에 연구된 해양 및 대기자료 품질처리를 위한 기계학습은 통상적으로 지도학습 설계에 초점이 맞춰져 왔다. 지도학습은 데이터의 입력-출력 쌍을 관찰하고, 입력을 출력으로 사상(mapping)하는 함수를 제시하는 학습 방법이다(Russell and Norvig, 2010). 때문에 지도학습은 출력값이 정해져 있는 회귀와 분류를 위해 주로 사용되는데, 일반적으로 품질처리를 위한 지도학습의 답은 참/거짓이나 이상치 분류 카테고리가 될 수 있다. 지도학습을 사용한 연구사례를 살펴보면, Castelão(2021)은 IOC-UNESCO 기준의 품질처리 표기(QC flag)가 주석으로 달린 13년간의 ARGO 외 profile 자료들을 대상으로 품질처리를 수행하여 이상값을 판별하였고, López-Lineros et al.(2014), Wang et al.(2019), 김 등(2019)은 고정된 기준치(threshold)를 설정하여 이상값을 탐지하였다. Just et al.(2018)은 위성자료의 에러 데이터셋을 구분한 후 학습을 진행하였고, Sciuto et al.(2009)은 특정 관측소의 강수자료의 참/거짓을 판별하기 위해 인접한 기준관측소의 강수 유무를 참값으로 사용하였다. Liu et al.(2020)은 품질처리 표기가 병기된 지하수 시계열 데이터에서 이상치를 탐지하는 모델을 설계하였다.
하지만 위와 같은 품질처리를 위한 지도학습 모델이 최적화하는 과정은 한가지 문제가 존재하는데, 바로 ‘데이터 불균형’이 고려되지 않는 점이다. 실제 관측되는 자료 중 이상치가 차지하는 비율은 매우 낮으며(Just et al., 2018: 0.02%; Castelão, 2021: 1% 미만), 이상치 비율이 낮을수록 모델이 가중치를 학습할 때 높은 비율을 차지하는 정상값에만 집중하게 만들어 이상값 탐지를 어렵게 한다(López-Lineros et al., 2014; Wang et al., 2019). Miau and Hung(2020)과 Kim et al.(2020)에서 사용한 방법은 데이터 불균형 이슈에서 자유로울 수 있는데, 전자는 관측 및 예측값을 이용하여 이벤트 발생 희귀도를 계산하는 Mahalanobis distance로 오측 가능성을 평가하였으며, 후자는 (σ: 과거 10분 자료의 표준편차)를 정상자료로 간주함으로써 품질처리를 수행하였다. Pastore et al.(2020)은 전술한 연구들과는 달리 비지도학습과 지도학습을 병용함으로써 비디오 데이터 내에서의 이상치 탐지와 플랑크톤의 종 분류를 동시에 수행하는 모델을 구성하였다.
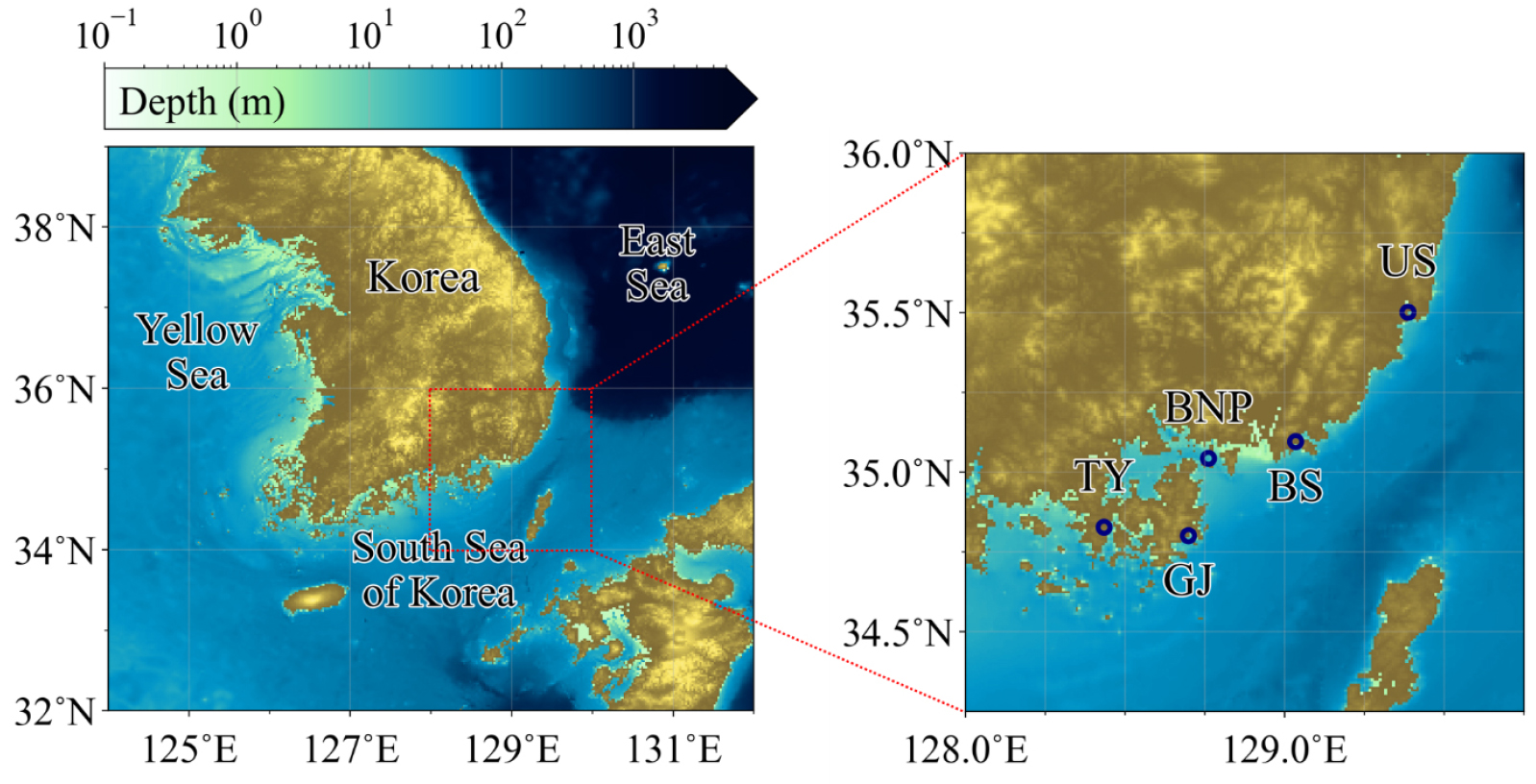
국내에서 수행된 관측자료 품질처리 관련 연구들은 담수 또는 기상 자료에 한정되어 있으며, 해수위 자료에 대한 연구는 선례를 찾아보기 어려운 실정이다. 육지에서의 유사 연구로는 김 등(2019)이 저수지 수위자료에 대한 품질처리를 수행하였는데, 임계치 모형을 사용함으로써 재해 등의 이벤트와 상관없이 고정된 기준치(threshold)를 사용하였다. 추가 유사 연구는 Kim et al.(2020)로, 고양시의 자동관측소에서 관측된 7개 항목 기상자료의 품질처리를 수행하였다. 이 연구는 다중 관측소의 시계열 데이터에 대해 기계학습 기반의 시간 및 공간 품질처리를 시도함으로써 수집자료의 평가 및 센서 오작동 예측의 기반을 마련하였으나, 시공간자료를 동시에 사용한 품질처리 모델의 성과를 제시하지 않았다. 본 연구의 목표자료인 우리나라 조위관측소 해수위 자료는 그 구성성분인 조석 및 잔차에 대해 시간상관성 뿐만 아니라 공간상관성이 높다. 따라서 본 연구는 시공간 자료를 사용한 해수위 자료의 인공신경망 품질처리 모델을 설계하였으며, 공간상관성이 높은 자료들을 입력세트로 사용하기 위하여 남동해에 밀접하게 위치한 5개 관측소에서 관측한 자료를 대상으로 교차실험을 진행하였다(Fig. 1).
2. 자료 및 방법
2.1 자료
본 연구 대상 자료는 조위관측소의 1분 간격 해수위 자료이며, 해당 자료는 국립해양조사원 바다누리 해양정보 서비스를 이용하여 수집하였다. 선정된 연구 대상지는 남동해안에 인접하여 위치한 5개 조위관측소(부산, 부산항신항, 거제도, 통영, 울산)로, 3년간(2018~2020)의 자료를 온전히 확보할 수 있는 관측소들로 구성하였다. 관측된 해수위 자료는 규칙적으로 변동하는 조석성분(천문조)과, 그 반대인 잔차성분(기상조, 조위편차)으로 분리될 수 있으며, 본 연구에서는 TASK-2000의 TIRA를 사용하여 해당 변동 성분들을 분해하였다(Murray, 1964; Bell et al., 1999). TIRA를 사용한 조화분해는 TASK-2000에서 제공하는 tira1yx.ctl 중 계절성을 나타낼 수 있는 Sa와 Ssa 분조를 제외한 60개 분조를 사용하였다. 모든 연구 정점에서의 조석 및 잔차 성분을 분석한 결과를 바탕으로 본 연구에서는 잔차를 해수위 이상치 탐지를 위한 변수로 선정하였다. Table 1에서 볼 수 있듯이, 2020년 관측 해수위를 기준으로 잔차의 표준편차는 10.3~12.4 cm로 비교적 균일하게 나타나지만, 대조차는 44.8~216.6 cm로 넓은 범위의 분포를 갖는다. 또한 해수위와 조석성분의 상관관계는 0.77~0.98로 나타나는데, 이는 조석성분이 해수위의 변동을 59%에서 96%까지 설명할 수 있음을 의미한다. 위 분석을 근거로 규칙적인 조석 성분을 품질처리 하는 것은 불필요할 뿐만 아니라, 변동폭이 큰 조석 성분을 포함한 해수위가 이상치 감지 인공신경망 학습에 사용될 경우 정상자료와 이상자료의 경계를 모호하게 만들어 이상치 탐지 능력을 저해할 수 있다고 판단하였다.
Table 1.
Summary of the characteristics of sea level components (BNP: Busan new port, BS: Busan, GJ: Geoje-do, TY: Tongyeong, US: Ulsan)
분리된 잔차 성분에 5차 버터워스 로우패스 필터(Butterworth lowpass filter)를 적용함으로써 5분 보다 짧은 주기의 잡음신호(noise)를 제거하였고, 잔차의 절댓값이 5σ(σ: 전체 자료의 표준편차)를 넘는 경우 해당 값은 명확한 오측으로 판단하여 제거하였다. 자료가 정규분포를 따르는 경우 5σ를 벗어날 확률은 약 1/1,744,278으로, 본 연구를 위해 수집된 모든 자료에서는 약 1/1,115의 확률로 출현하였다. 전처리된 자료에서 5분 미만의 연속된 결측에는 선형 보간을 적용하였으며, 위의 과정들을 거친 5 개 정점의 1분 간격 데이터를 사용함으로써, 이상치 탐지를 위한 모델설계 과정을 더욱 탄탄해(robust) 질 수 있도록 한다. 마지막으로 잔차의 변동량(직전시간 대비 현재시간의 잔차 증가량) 인자를 추가함으로써 해당 모델이 기압점프, 태풍 등의 이벤트로 인한 잔차 변동을 더 잘 모의할 수 있도록 하였다.
전처리를 마친 5개 정점의 자료는 결측 및 제거된 오측으로 인해 상이한 길이를 갖는다(Table 2). 인공신경망 모델 설계를 위한 데이터셋 구성은 후술할 연구 방법에서 제시한다.
Table 2.
Length of dataset at the five tide gauge observatories during 2018-2020 (BNP: Busan new port; BS: Busan; GJ: Geoje-do; TY: Tongyeong; US: Ulsan. Unit: ea.)
Location Year | BNP | BS | GJ | TY | US |
| 2018 | 515,221 | 524,368 | 518,260 | 519,770 | 517,120 |
| 2019 | 517,571 | 524,619 | 504,913 | 525,355 | 525,533 |
| 2020 | 496,207 | 521,846 | 510,358 | 526,239 | 513,753 |
2.2 방법
2.2.1 앙상블 모델 설계
Opitz and Maclin(1999)은 앙상블(ensemble) 기법을 기계학습에 적용할 경우에, Linares-Rodriguez et al.(2013)과 Fourrier et al.(2020)은 인공신경망에 적용할 경우에 모델의 신뢰도(reliability) 및 탄탄함(robustness)이 두드러지게 향상됨을 밝혔다. Guan and Plötz(2017)는 이를 본 연구에서 사용된 LSTM (Long-Short Term Memory)을 사용하는 경우에 대해서도 증명한 바 있다. 또한 품질처리를 위해 기계학습을 사용한 연구 중 Just et al.(2018)과 Yu and Xi(2009)는 앙상블 기반 모델을 구성함으로써 모델 성능을 제고하였다. 이에 본 연구에서도 앙상블 모델 설계를 바탕으로 연구의 신뢰도를 높일 뿐만 아니라 실제 현장에서의 실시간 해수위 이상치 탐지 시 활용성을 제고할 수 있도록 하였다.
본 연구는 기계학습을 위한 앙상블 학습 유형 중 보팅(voting) 기법을 사용하였는데, 다수의 모델이 예측한 결과값을 최종 결과로 선정하는 하드 보팅 방식을 차용하였다. 해당 연구의 앙상블 모델은 다음과 같은 과정을 통해 이상치 탐지를 수행한다. 총 5개 정점 중 레이블(label; 인공신경망 학습에서 정답이 되는 표기를 의미함)이 되는 해수위 관측데이터를 목표데이터(target data)로 구성할 한 점을 선정한 후, 남은 4개 정점자료로 조합할 수 있는 모든 경우()의 모델을 구축한다. 해당 설계는 가능한 모든 조합의 모델을 사용함으로써, 일부 정점에서의 결측에도 대응할 수 있는 부가적인 장점을 가지게 된다. 목표 정점별로 각각 수립된 15개 모델은 다시 훈련자료(training set)가 홀수일자, 짝수일자의 데이터로 각각 구성됨으로써 30개 모델로 확장된다. 학습데이터셋을 2분할하는 것은 K-겹 교차검증(k-fold cross validation) 방법(k=2)과 유사한 형태를 취하게 되며, 이러한 모델 구성은 과적합(overfitting)을 방지함으로써 모델의 일반화를 유도할 수 있다.
학습이 완료된 모델들은 각각 모의된 해수위 값을 만들 수 있다. 본 연구는 이를 정상 범주의 해수위()로 간주하였고, 각 모델별로 모의한 해수위와 관측값()의 오차편차()를 사용하였으며, 시행착오(trial and error) 과정을 통해 인 관측값을 이상치로 판별하도록 설계하였다. 마지막으로 특정 시점의 관측값에 대해 전체 모델이 이상치 여부를 투표하게 되고, SeaDataNet과 GTSPP에서 사용하는 품질처리 표기를 부여하였다(UNESCO, 2013). 투표에 참여한 모델의 90% 이상이 해당 관측값을 이상치로 판별했을 경우 이상치(Bad data), 70%~90% 일 경우 이상치 추정(Probably bad data), 50%~70%일 경우 정상자료 추정(Probably good data) 단계로 설정하였다. 정상자료 추정 단계는 과반수 이상의 득표에도 불구하고 이상치로 확신할 수 없는데, 해당 연구에 사용된 자료가 품질처리 전의 원시데이터를 사용하는 점에서 기인한다. 이상치가 포함된 학습 입력자료는 품질이 떨어지는 해수위를 모의하게 되는데, 해당 모의자료의 개수는 앞에서 설명한 모델 조합에 대해 (n+1)/2로 나타난다. 즉, 15개 조합 구성 시 8개의 조합에서 이상치를 포함한 입력자료가 사용되는 것과 같다. 추가적인 이유로는 기상 이벤트에 의한 해수위의 급변동을 이상치로 확신하지 않기 위함이다. 사용된 자료들의 교차상관분석 결과 각 관측소의 잔차 변동성은 최대 ±1시간의 선행-후행(lead-lag) 관계에 있었는데, 표준화된 모델 세트를 구성하기 위해 해당부분은 고려하지 않았다.
2.2.2. 인공신경망 모델 설계
본 연구는 잔차 자료 간에 높은 공간상관성을 보이는 것을 고려하여 인접한 5개 연구 정점에 대한 입력세트를 구성하였으며, 시간상관성 또한 고려하기 위해 LSTM을 사용하였다. LSTM은 시계열을 고려하는 인공신경망 기법인 재귀신경망(Recurrent Neural Network; RNN) 기법 중 순차자료(sequence data)의 장기 기억 능력을 향상시킨 모델이다(Hochreiter and Schmidhuber, 1997). LSTM의 입력자료 배열은 [배치 사이즈(batch size), 순차(sequence), 특징(feature)]로 구성되며, 각각 순서대로 가중치 갱신에 사용될 병렬연산 행 수, 고려될 시계열의 길이, 입력자료의 종류를 의미한다(Fig. 2). 배치 사이즈는 1 에포크(epoch)당 200회의 연산이 진행되도록 데이터 길이에 따라 유동적으로 부여하였고, 순차는 모의 시점의 전후 15분을 포함한 31분으로 설계하였다. 모의 시점 후방 15분까지의 자료를 입력자료로 사용하였고, 해당 입력자료는 5분 로우패스필터 된 자료이므로 본 모델은 준실시간으로 전송되는 수위 자료의 이상여부를 20여 분 내에 모니터링 할 수 있다. 특징은 모델에 입력되는 타 관측소 정점 수˟2(잔차, 잔차의 변동량)로 구성된다. 학습데이터셋은 앙상블 모델 설계파트에서 설명한 것과 같이 홀수, 짝수일자로 나뉘며 각각 검증데이터 셋은 그 반대이다. 각 관측소 자료가 갖고 있는 결측 시점이 다르기 때문에 인공신경망 학습에 사용된 시계열의 총 길이는 모델별로 상이하다.

Fig. 2.
Structure of LSTM model1). The three-dimensional structure consists of batch size, sequence, and feature, while the two-dimensional structure consists of batch size and feature. Question mark indicates flexible batch sizes depending on data length.
3. 결 과
3.1 학습 검증 결과
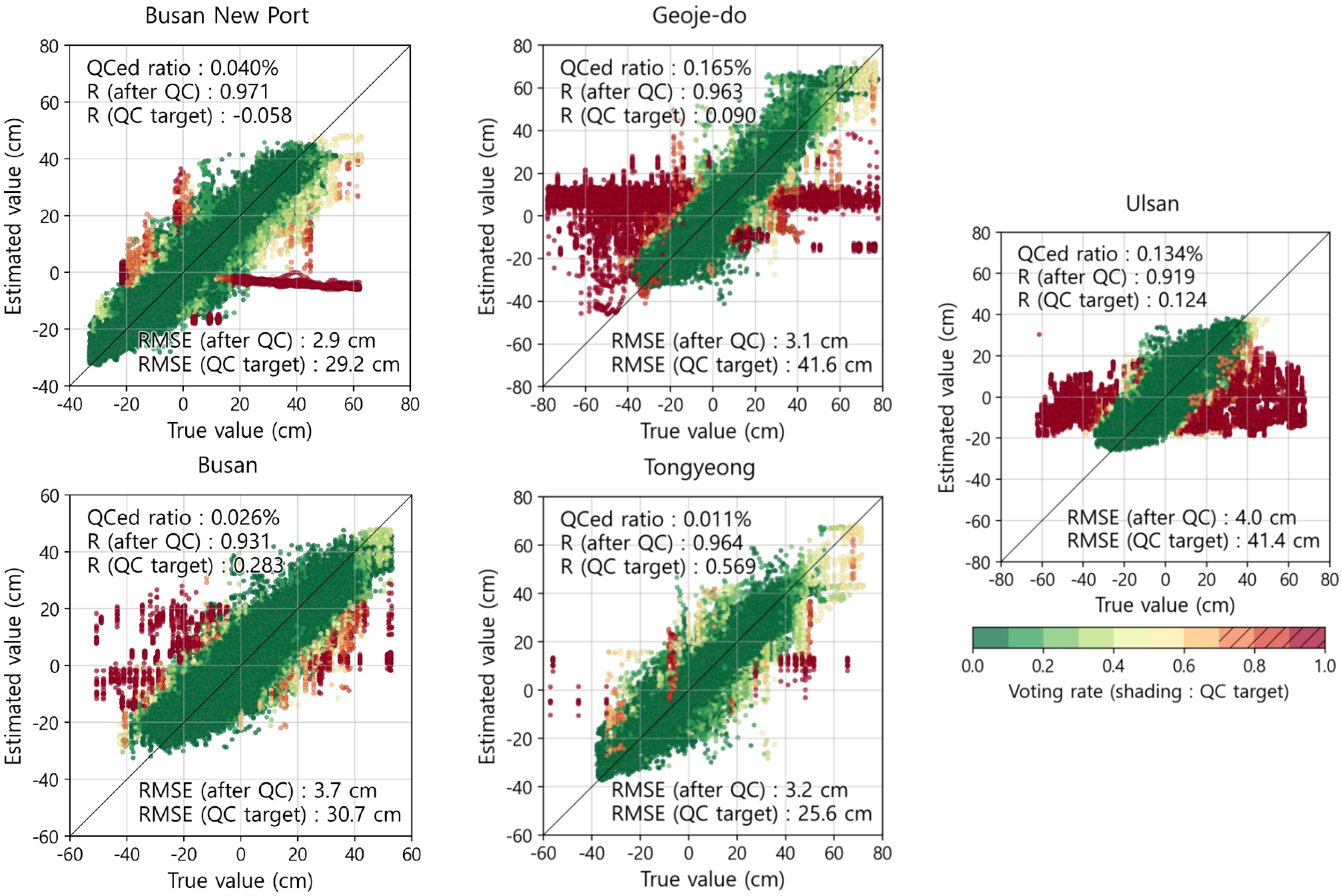
전처리된 관측 해수위자료와 모델이 추정한 해수위를 비교함으로써 해당 모델의 검증을 수행하였다(Table 3, Fig. 3). 보팅 기법을 적용하여 판단된 이상치는 통영관측소에서 가장 낮은 0.011%, 거제도관측소에서 가장 높은 0.165%의 비율로 나타났다. 관측소별 이상치를 처리한 관측값(QCed value)과 30개 모델 추정치와의 평균 상관계수는 0.919~0.971로 나타났으며, 평균 RMSE는 2.9~4.0 cm로 본 연구에서 수립한 모델이 관측값을 잘 모의하고 있음을 알 수 있다. 가장 낮은 상관계수(높은 RMSE)를 가지는 울산 관측소는 해당 연구 정점들 중 최동북단에 위치하고 있어 타 정점들의 시계열과 상관성이 상대적으로 작게 나타난 정점이다(교차상관분석 결과는 본 연구에 싣지 않음). 이상치(QC targets)와 추정치와의 상관계수는 -0.058~0.569로, RMSE는 25.6~41.6 cm로 나타나는데, 이상치 판별 결과는 다음 절에서 상세히 다룰 예정이다.
Table 3.
Summary of model verification results at the five tide gauge observatories (BNP: Busan new port; BS: Busan; GJ: Geoje-do; TY: Tongyeong; US: Ulsan)
3.2 품질처리 검증 결과
본 절에서는 검증이 완료된 모델에서의 해수위 오측 품질처리 결과를 제시하였다. 오측은 상시 존재하는 것이 아니므로 품질처리가 수행된 시간대와 특이사항이 있는 시간대를 Fig. 4에 도시하였으며, 오측으로 오인되어 참값이 제거될 수 있는 사례를 Fig. 5에 제시하였다. 해당 연구는 앙상블 기법을 차용하고 있어 오측 판단에 사용된 모델 개수 또한 중요하다. 모델 입력자료가 결측일 경우 투표 결과를 얻지 못하게 되며, 통상 한 관측소의 결측은 30개 모델 중 16개 모델의 결과를 NaN (Not a number)으로 송출하게 된다. 이러한 이유로 그림 상단에 투표에 참여한 모델이 적은(1~5개; Fewer mdl.) 경우와, 결측 또는 0개 투표로 모델이 성립하지 않는 경우를 표기하여 의사결정에 참고할 수 있도록 하였다.
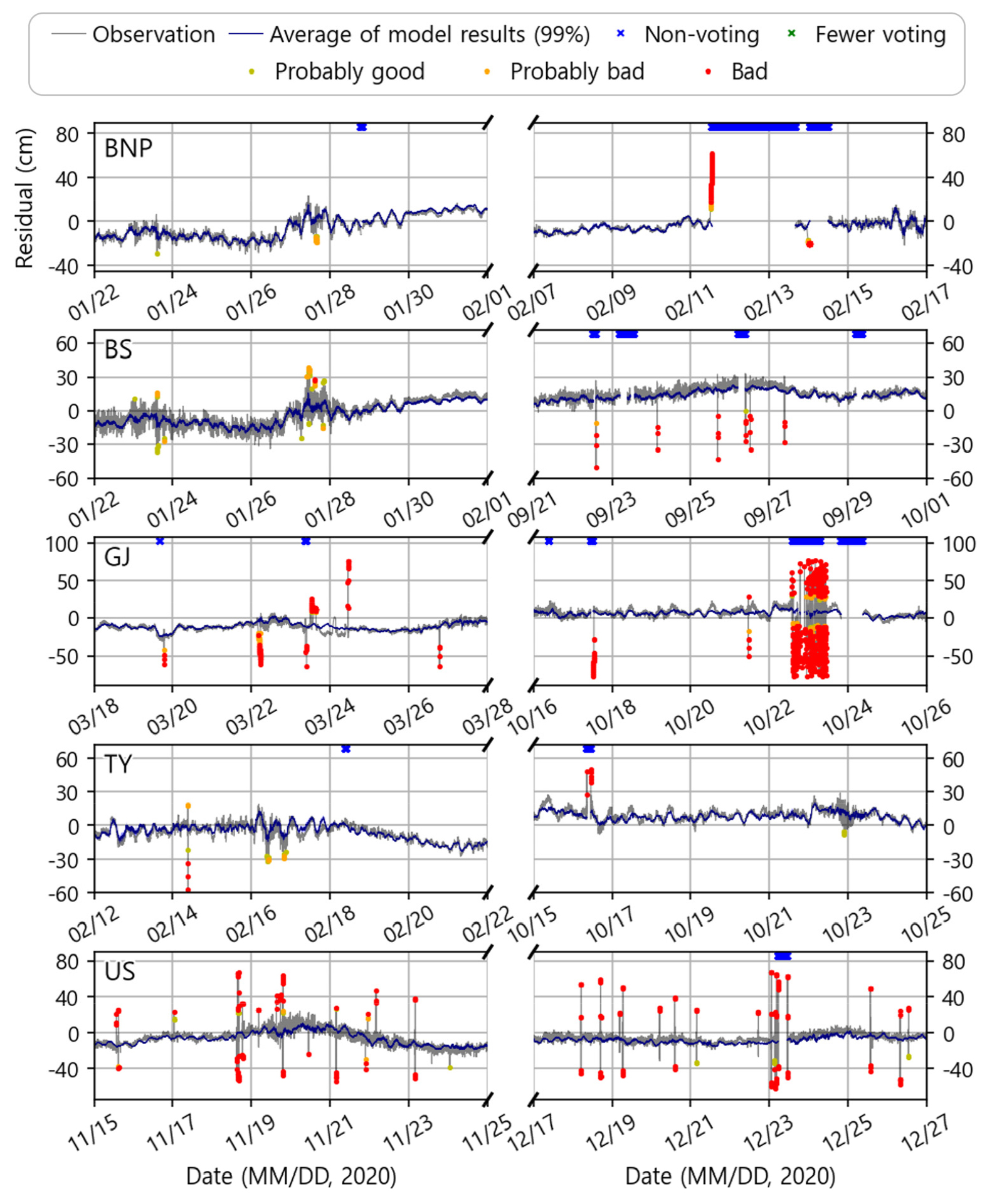
Fig. 4.
Time series of validated model results in normal times. The gray and navy solid lines mean the observations and the average value of the model results (filled with blue: 99% confidence interval), respectively. For decision making, fewer (1 to 5) voting and non-voting are represented by green and blue scissors, respectively. Depending on the voting rate with the model, bad, probably bad, and probably good are marked with red, orange, and yellow dots, respectively.
해당 모델은 전반적으로 평시의 오측을 잘 감지하고 있으며, 불필요한 오측 처리를 하지 않도록 하고 있음을 볼 수 있다(Fig. 4). 2020년 1월말경 부산항신항과 부산 조위관측소에 공통적으로 단주기 해수면 진동이 관측되었는데, 이상신호로 탐지될 수 있는 해당 값들을 본 모델은 정상 범주로 판단하였다. 하지만 부산, 울산 관측소에서의 튐 값 일부를 탐지하지 못하거나 낮은 오측 확률을 부여하는 경우를 볼 수 있는데, 이러한 결과의 주된 원인은 본 연구가 ‘표준화된 준실시간 오측 탐지 모델 수립’을 목표로 하는 것에서 기인한다. 해당 연구는 준실시간으로 모델이 수행될 수 있도록 입력자료 구성 과정에서 비교적 짧은 주기인 5분의 로우패스 필터를 적용하였고, 이 과정에서 미처 제거되지 못한 단주기 해수면진동은 참값으로 남아있게 된다. 본 연구는 문제의 단순화를 위해 비교적 간단한 인공신경망 모델을 수립하였으며, 이러한 단주기 해수면 진동까지 고려하지 않은 학습 모델은 해당 진동을 허용오차로 남겨둔다. 추가로 앞절에서 언급한 것과 같이 해역 전반에서 나타나는 단주기 해수면진동 및 기상재해 등의 이벤트에 대하여 덜 민감하게 반응할 수 있도록 함과 동시에, 설계의 표준화를 위해 전 관측정점에서 동일한 조건()을 적용했기 때문에 나타난 결과이다.
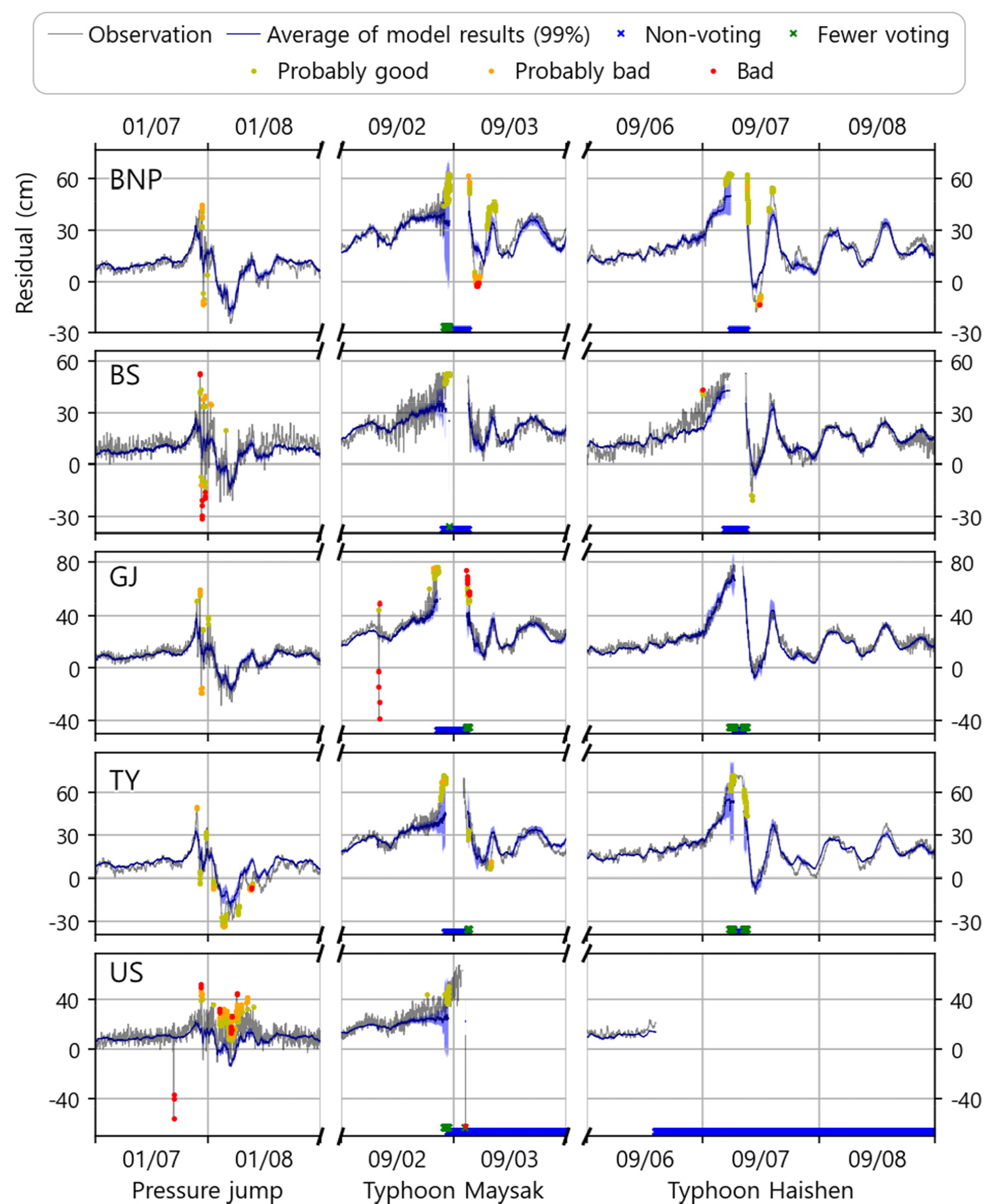
이상치 탐지 및 품질처리 모델을 수립할 때, 정상자료에서 이상신호를 분류해내는 것만큼이나 중요한 것은 바로 정상신호의 보존이다. 본 연구에서는 정상관측값의 보존 사례를 다음과 같이 검토했다. 2020년에는 중단기 해수면변동 이벤트가 세 차례 있었는데, 1월에 발생했던 기압점프 통과, 9월에 내습한 태풍 마이삭과 하이선이 그 사례이다(Fig. 5). 큰 시간 스케일에서 볼 때 다른 기상정보가 없다면 12시간에 준하여 발생하는 해당 이벤트 전체를 이상값으로도 판단할 가능성이 있으며, 이벤트 내부의 단기해수면 진동 또한 이상값들로 판별할 수 있다. 본 연구는 인근 조위관측소의 해수위 시계열을 입력자료로 함으로써 공간적인 상관관계를 학습할 수 있게 설계되었고, 앞절에서 언급한 것과 같이 덜 보수적으로 판단하는 알고리즘을 구축함으로써 이벤트 전체를 오측으로 판단하지 않을 수 있게 하였다. 하지만 이 같은 노력에도 불구하고, 해당 이벤트의 자료들은 다소 높은 오측 확률을 가지고 있는데, 부산 관측소의 기압점프 통과 사례에서 볼 수 있듯이 일정수준 이상의 진동은 다소 높은 오측 확률을 가지는 것으로 판별되었다. 또한 타 관측소의 동시결측이 많았던 거제도의 태풍 마이삭 사례에서도 적은 기표수로 인해 상대적으로 낮은 신뢰도에서 높은 오측 확률을 보이게 된다. 이부분은 본 연구의 한계점으로, 연구 전체 데이터 중 이벤트가 극히 일부분을 차지하고 있기 때문에 그 경향성을 충분히 학습하지 못했기 때문이다. 추가로, 울산 관측소의 기압점프 통과 사례에서는 평균 모의값이 음의 편향을 보이는데, 이는 3.1절에서 언급한 것처럼 외곽에 위치한 정점 특성상 충분한 입력자료가 확보되지 못했기 때문인 것으로 판단된다.
3.3 학습기간 외 기간(2018, 2019)에의 적용
인공신경망 모델의 데이터셋은 크게 훈련자료(training data)와 평가자료(test data)로 분리되는데, 훈련자료는 가중치 갱신에 직접 사용되거나 학습을 조정, 검증(validation)하는데 사용된다. 반면 평가자료는 학습에 완전히 독립적인 데이터셋으로써 모델의 범용성을 평가하는데 사용된다. 인공신경망 모델의 강점 중 한가지는 학습된 모델(가중치 세트)을 지속적으로 사용할 수 있는 것에 있으며(재학습이 불필요), 학습에는 상당한 시간이 필요한 반면에 학습된 모델을 재사용하는 것은 시간소요가 거의 없다. 이 점을 활용하기 위해 본 연구에서는 비교적인 단기 데이터로 학습된 모델이 다른 장기 데이터에도 적용될 수 있는지 검토하였다. 이를 위해 2020년 한 개 년도의 자료만을 사용해서 학습을 진행하였고, 학습된 모델을 2018, 2019년 자료에 적용하였다. 다시 말하면, 본 연구에서는 2020년 수위 시계열이 훈련자료로, 2018년과 2019년 수위 시계열이 평가자료로 사용되었다.
평가자료의 검증 또한 3.2절과 같은 방식으로 실시간 데이터 품질 모니터링 상황을 가정하여 평시 및 이벤트시의 오측 확률을 제시하였다. 학습에 참여하지 않은 2018년과 2019년도 자료를 적용했을 때 또한 전반적으로 평시의 오측을 잘 감지하고 있으며, 불필요한 오측 처리를 하지 않음을 볼 수 있다(Fig. 6). 학습되지 않은 이벤트가 있을 때의 모델의 반응을 살펴보기 위하여 2018년 2월말의 기압점프 통과, 2018년의 태풍 솔릭, 2019년의 태풍 타파스 사례를 제시하였다(Fig. 7). 훈련자료의 이벤트시에 낮은 오측 확률이 제시된 것과 달리, 해당 이벤트 시기들의 해수위 모의는 실측값을 잘 모사하지 못하여 높은 오측 확률을 보였으며, 특히 태풍 솔릭은 이벤트 전반에서 높은 오측 확률이 나타났다. 이 부분은 3.2절에서 언급한 이벤트 데이터에 대한 본 연구의 한계점이 확장된 것으로, 해당 문제는 4.1절에서 자세히 다룬다.
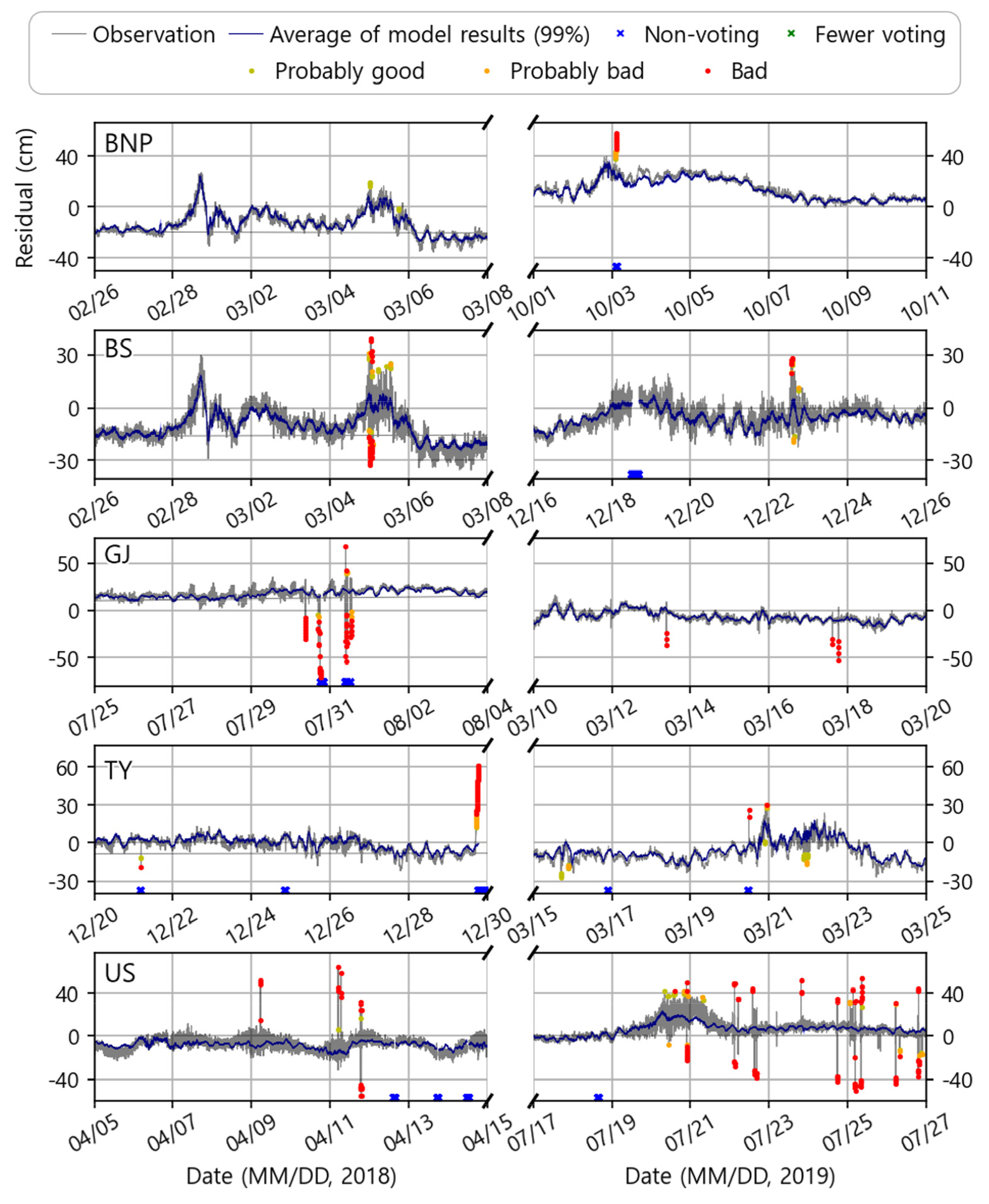
Fig. 6.
Time series of test data from 2018 to 2019 applied to the validated model trained with 2020 data (in normal times). Legend is the same as Fig. 4.
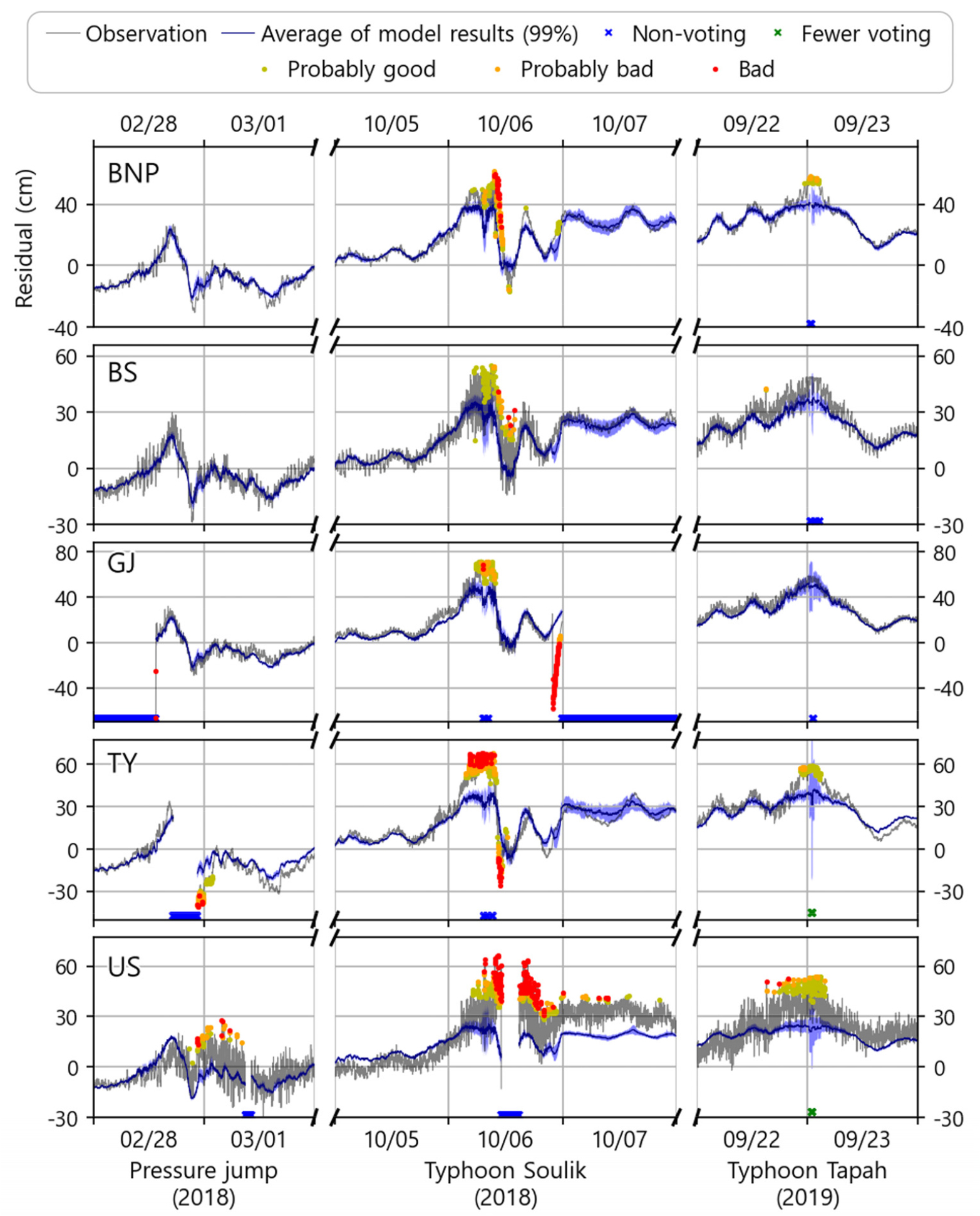
Fig. 7.
Time series of test data from 2018 to 2019 applied to the validated model trained with 2020 data (during the oceanic events). Legend is the same as Fig. 4.
4. 토 의
4.1 과적합 및 과소적합 문제
앞절에서 2020년도 자료로 학습이 완료된 모델에 2018년과 2019년도 자료를 적용한 결과를 살펴보았다. 본 절에서는 해당 개념을 확장하여 2018년도와 2019년도 자료로 각각 학습한 모델 또한 적용해 봄으로써 본 연구에서 발생할 수 있는 과적합(overfitting)과 과소적합(underfitting) 문제를 검토하고자 한다.
본 연구는 주변 정점의 관측값으로부터 목표 정점의 일반적인 해를 찾음으로써 이상치를 판별하도록 설계되어 있는데, 학습 과정에서 이상치 또한 정답으로 만들어 내는 것이 해당 연구에서의 과적합 과정이다. 제시한 과적합 예시는 거제도 조위관측소에서의 모델 결과이며, 훈련자료의 연도를 각 열에, 평가자료의 연도를 각 행에 표현하였다(Fig. 8). 학습연도와 적용(평가)연도가 같은 대각성분은 일부 구간에서 모델이 이상치에 과적합되어 타 연도의 학습모델보다 더 낮은 오측 확률을 부여하는 경향을 보였으며, 학습연도와 적용연도가 다른 경우에는 해당 구간에서의 과적합을 피하여 적절한 오측 확률을 제시하는 것을 볼 수 있다.
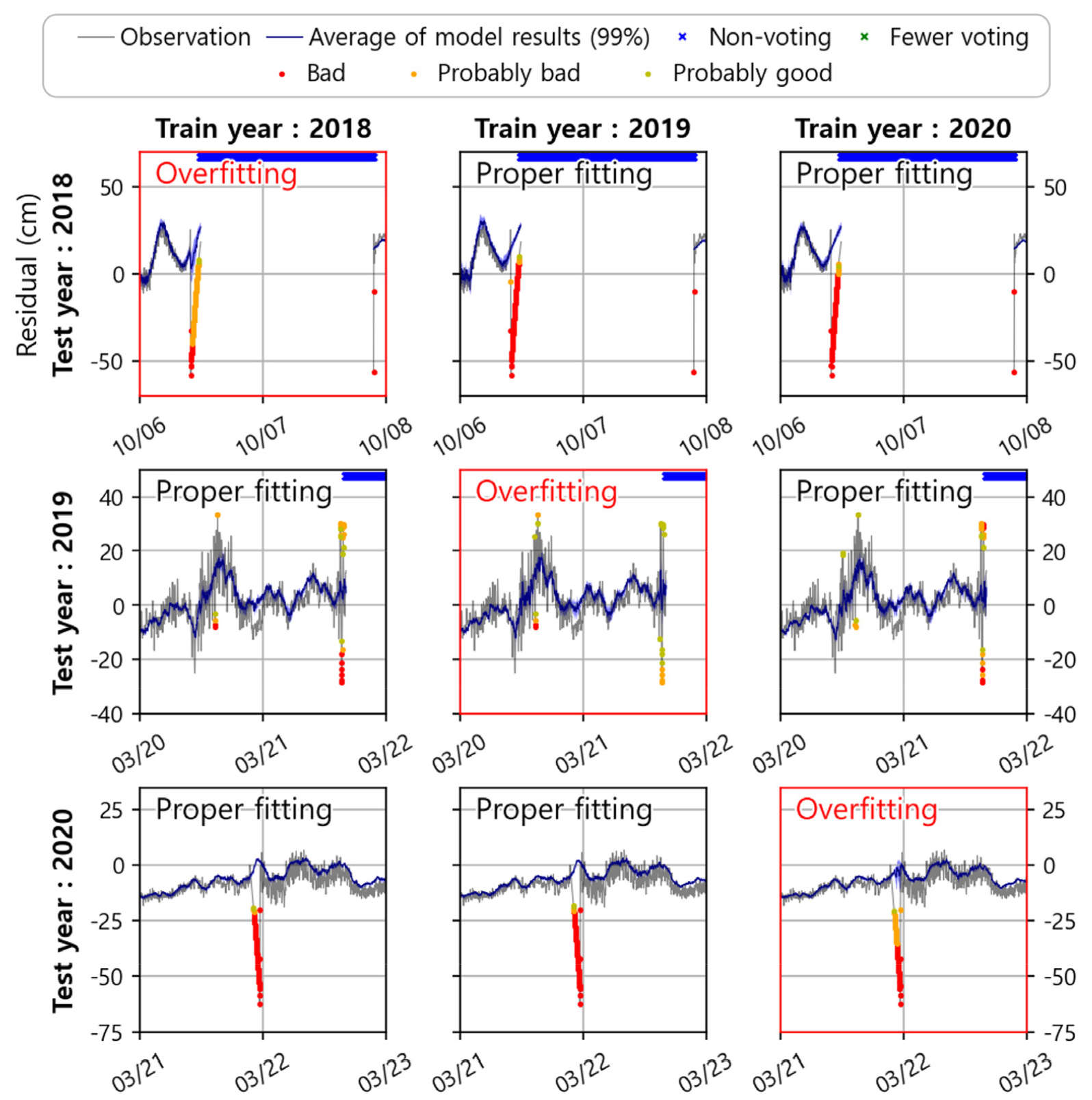
Fig. 8.
Test for overfitting cases depending on the year of training data. The horizontal axis represents the training year and the vertical axis represents the test year, and hence the overfitting can be seen in the diagonal components (red boxes; the same year of training and test). Legend is the same as Fig. 4.
이러한 과적합을 방지하기위해 많은 기술적 방법론들이 보고되어 왔지만, 본 연구의 설계과정을 고려했을 때 다음과 같은 간단한 추가 설계로 과적합 문제를 해소할 수 있을 것으로 예상된다. 첫 번째로, 품질처리 된 데이터를 사용함으로써 새로운 모델을 학습하는 방법이다. 본 연구에서 사용된 데이터는 원시데이터에 준하는 상태로, 오측값을 거의 모두 포함하고 있으며 이 부분이 본 연구에서 과적합 문제를 야기시키는 주요 원인이다. 본 연구에서 제안한 모델은 준실시간 수위 품질 모니터링을 위하여 설계되었지만, 일정 수준의 품질처리 또한 가능하다. 따라서 현업에서 품질처리가 수행된 자료를 사용하거나, 해당 모델을 사용하여 대략적으로 품질처리를 선 수행한 후 재학습 시에 과적합을 일정부분 해소할 수 있다. 두 번째는 앙상블 멤버를 늘리는 방법이다. 현재 설계에서는 앙상블 멤버 중 절반이 해당 과적합을 유도할 수 있다. 따라서 현재 짝, 홀수 일자로 이분할 한 모델을 더욱 세분화하거나, 연도별 모델을 추가 멤버로 구성하는 등의 추가 설계가 진행된다면 과적합을 유도하는 모델의 투표율을 줄일 수 있게 될 것이다.
과소적합은 과적합에 반대되는 개념으로서, 이미 있는 훈련자료에서 학습을 하지 못한 상태를 의미한다. 본 연구에서의 과소적합은 주로 기압점프와 태풍이 지나가는 이벤트에서 발생하는데, 학습연도와 적용연도가 다를 경우 더욱 많은 과소적합 경향을 보인다(Fig. 9). 과소적합은 일반적으로 데이터의 양이 적거나, 입력 특징이 부족하거나, 모델이 너무 단순할 때 발생할 수 있는데, 본 연구에서의 과소적합은 두 전자에 의한 것으로 보인다.
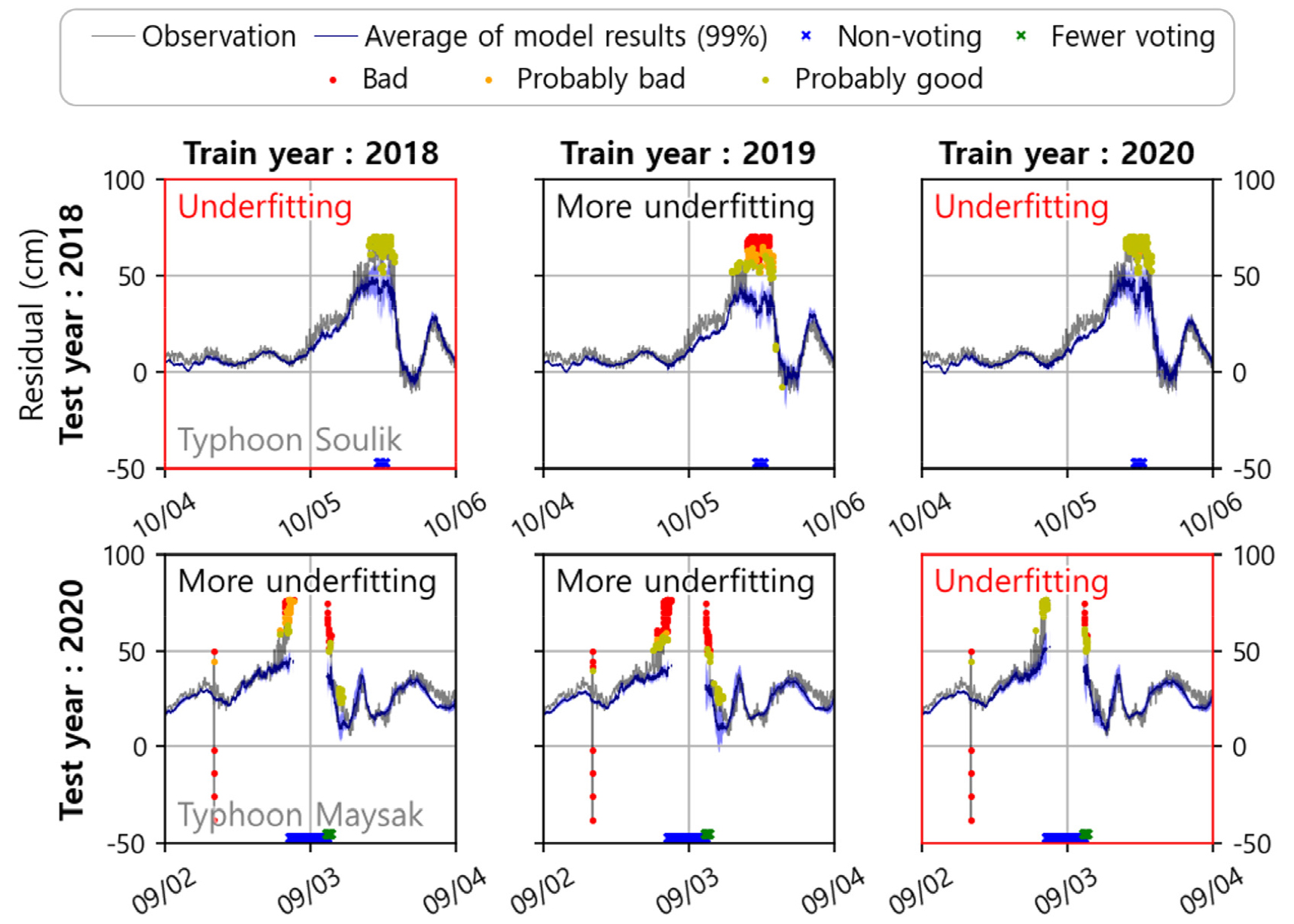
Fig. 9.
Test for underfitting cases depending on the year of training data. The x-axis represents the training year and the y-axis represents the test year. At very few oceanic events, underfitting may occur, especially in untrained years (black boxes). Legend is the same as Fig. 4.
평시 데이터보다 빈도가 절대적으로 적은 이벤트 데이터의 모니터링은 본 연구의 가장 큰 약점인데, 이 문제를 완화하기 위해서 다음과 같은 방법을 고려할 수 있다. 첫 번째는 가상 데이터의 보강이다. 서론에서부터 언급해온 데이터 불균형 문제는 기계학습의 숙제로, 데이터 증강(data augmentation) 기법을 사용함으로써 해당 문제를 완화할 수 있다. 하지만 극히 일부인 이벤트 데이터를 복사하는 것에는 한계가 있으므로, 다음 제안이 더욱 현실적일 것이다. 두 번째 고려사항은 기상자료를 학습인자에 추가하는 것이다. 기상 이벤트는 강제력으로서 해수면 변동 이벤트에 반드시 선행한다. 따라서 목표 정점의 해수위와 인근 기상관측소의 기압, 바람 등의 상관관계를 검토한 후, 입력자료로 추가한다면 이벤트시의 과소적합을 다소 완화할 수 있을 것으로 예상한다.
4.2 Time step 선정 문제
시계열을 다루는 재귀신경망 계열 모델(SimpleRNN, LSTM, GRU 등)은 순차(sequence), 즉 입력 받을 시계열 길이 또한 주요 매개변수이다. 본 연구는 품질처리시점 전후 15분 자료를 사용하였는데, 순차의 설정에 따른 모델 결과를 비교하기 위해 다음과 같은 비교실험을 진행하였다. 본 연구에서 진행한 실험을 대조군(control model; Case0)으로 하였으며, 실험군(treated model)은 기타 조건(데이터셋 설계, layer 및 node, activation function 등)을 동일하게 설계하되 대조군보다 짧은 순차(Case1)와 긴 순차(Case2)로 설정하였다. Case1의 경우 시계열을 고려하지 않으므로 단순한 완전 연결 인공신경망(Fully connected ANN; FC-ANN) model을 사용하였다(Table 4).
Table 4.
Configurations of the case studies for the impact of time step change
| Model case | Time step | Remark |
| Case0 | ±15 minutes | Result of Section 3 |
| Case1 | ±0 (at the same time) | Using FC-ANN |
| Case2 | ±1 hour | - |
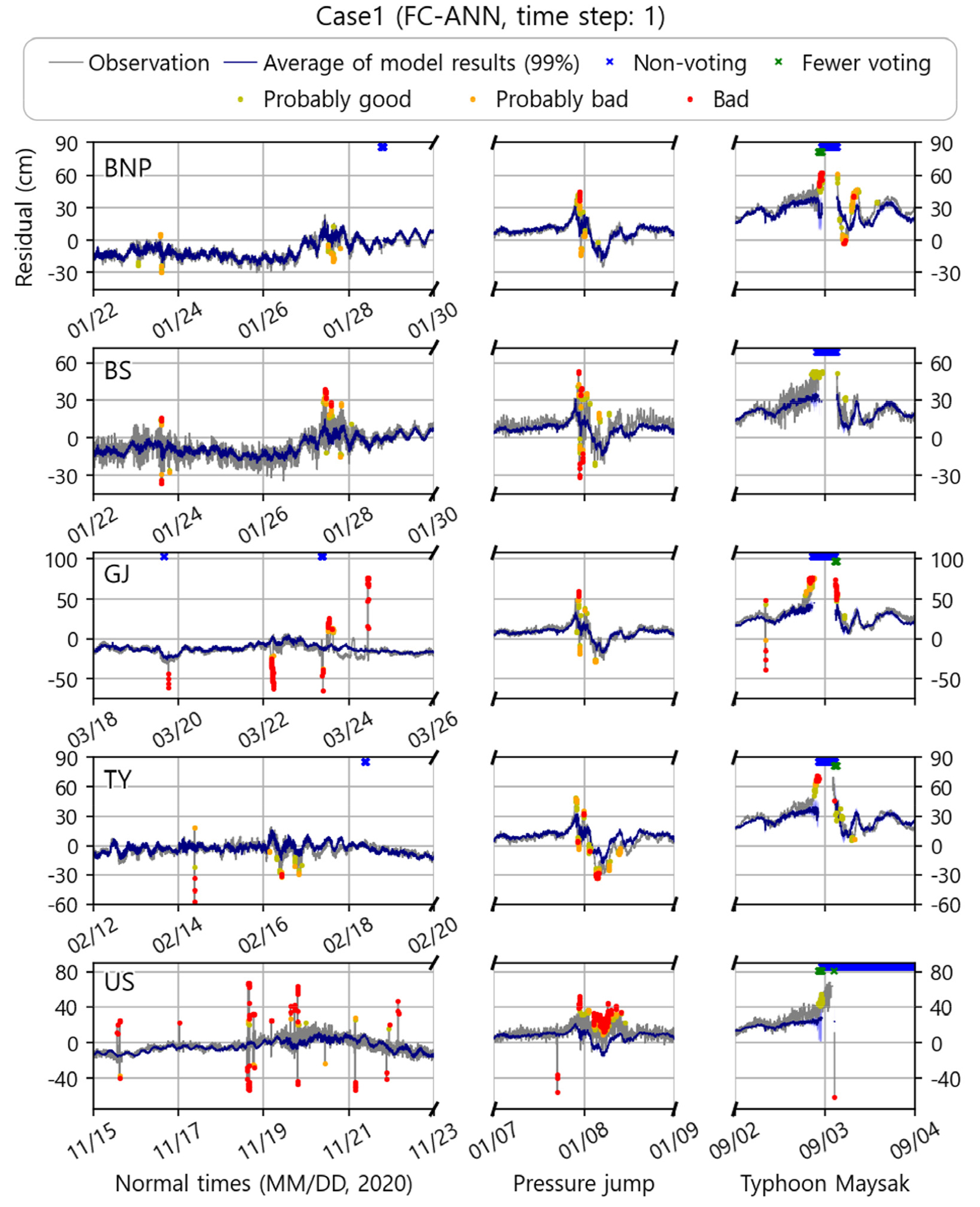
모델 수행 결과, Case1은 Case0에 비해 모든 연구 정점에서 이상치 판단 비율(QCed ratio)이 4.8~254.5% 증가하였으며, 이상치를 처리한 관측값(QCed value)과 모델 추정치와의 평균 상관계수는 모든 정점에서 공통적으로 Case1에서 소폭 감소하였다(Table 5). 이 결과는 Case1의 모델이 정상 범주의 데이터를 이상치로 과하게 판단한 함과 동시에 이상치 판정에는 낮은 정확도를 보임을 시사하고 있다. Case1은 모델들이 추정하는 값들 간의 분산(variation)이 작게 나타나는데(유사한 결과를 내놓으므로 모델 추정치의 평균이 Case0에 비해 큰 변동폭을 가짐), 이는 앙상블의 의미를 퇴색시키며 모델이 더 보수적인 오차평가를 수행하게 한다. 이러한 이유로 평시의 단주기 해수면 진동은 오측으로 판단되며, 해양재해 등의 기상 이변시에는 그 영향이 더 크게 나타나는데, 이는 시계열의 시간상관성을 가중치에 포함하지 못하는 FC-ANN 모델이 정점 간에 시차를 갖고 전파되는 해수위 변동을 고려하지 못하는 데서 기인하는 것으로 추정된다(Fig. 4, Fig. 5, Fig. 10).
Table 5.
Summary of quality control results for the three model cases
Case2는 Case0과 비교했을 때, 부산 조위관측소를 제외한 모든 정점에서 이상치 판단 비율이 감소하였으며, 평균 상관계수는 전 정점에서 소폭 증가했음을 볼 수 있다. 해당 결과는 이전 절에서 설명한 과적합 문제로 설명이 가능하다. Case2의 모델은 더 긴 시계열의 시간상관성을 가중치에 저장할 수 있으며, 그렇기 때문에 계산되는 파라미터(parameter) 또한 증가한다. 이는 모델이 목표자료에 더 잘 적합(fitting)되게 하는 반면, 과적합 문제 또한 동반한다. Case2 모델은 부산을 제외한 모든 관측소에서 과적합 된 결과를 보이는데, 제시한 평시 시계열 중 거제도 조위관측소에서 그 문제점이 가장 두드러지게 나타나는 것을 볼 수 있다. 이러한 과적합은 이벤트시에 조금 다른 역할을 하는데, 데이터불균형으로 인해 평시로 최적화된 모델이 이벤트시에 넓은 범위의 추정값을 만들어내므로 개별 모델은 큰 오차를 가질 수 있으나, 모든 모델이 투표 시 낮은 오측 확률을 제시할 수 있게 된다(Fig. 4, Fig. 5, Fig. 11). 비록 Case2 모델이 해양재해 등의 발생시 관측되는 정상범위 값에 낮은 오측 확률을 제시하지만 그 과정이 의도한 방향이 아니었을 뿐만 아니라, 재해 시 빈번하게 발생하는 결측은 판별 모델 개수를 줄이므로, 그에 따라 커진 오차범위 또한 무시할 수 없다. 무엇보다 Case2 모델의 가장 큰 문제는 전후 한시간 자료를 입력하는 것에 있다. 해당 조건은 결측이 있을 시, 그 후 한시간 동안은 해당 자료를 사용하는 모델이 작동할 수 없다는 치명적인 단점을 가지고 있어, 전후 15분을 사용하는 대조군 모델과 비교했을 때 준실시간 이상치 모니터링의 의미 또한 퇴색되는 것을 알 수 있다.
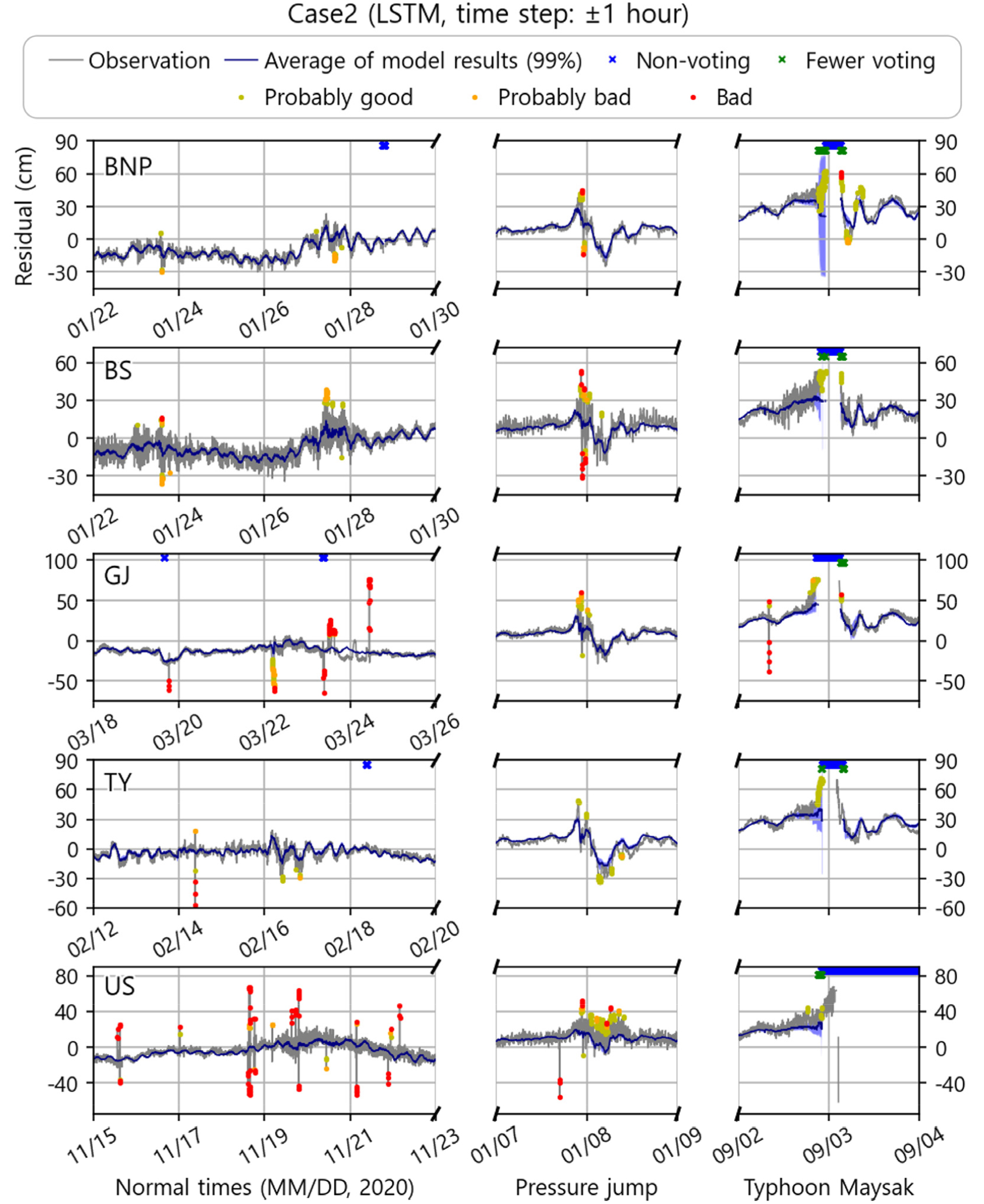
Fig. 11.
Time series of Case2 (LSTM, time step: ±1 hour) model results. Legend is the same as Fig. 4.
따라서 위 결과를 종합해 보았을 때, 준실시간 이상치 모니터링을 위해서는 시계열을 고려하는 재귀신경망 계열의 모델이 필수임을 알 수 있었으며, 이상파랑 등의 전파속도를 고려하여 적절하게 긴 순차 길이를, 과적합을 방지하며 실시간의 의미를 담을 수 있도록 적절하게 짧은 순차 길이 선정이 필요하다는 것을 확인할 수 있었다.
4.3 일반적인 품질처리, 이상치 모니터링 방법과의 비교
품질처리 또는 이상치 모니터링에 사용되는 일반적인 방법들이 인공신경망을 사용한 방법에 준하는 이상치 분해능을 갖는다면, 컴퓨팅 재원이 날로 좋아지는 현 시점에서 본 연구의 효용 가치는 하락할 수밖에 없다. 본 절에서는 해당 연구의 효용성을 재차 확인하기 위해 일반적으로 사용되는 품질처리, 이상치 모니터링 방법을 적용하여 결과를 비교하였다(Fig. 12). 첫 번째로, 널리 알려진 경험적 규칙(3σ 규칙)을 적용하고자 하였으나, 태풍, 기압점프 이벤트 등의 정상신호들을 모두 이상치로 취급하게 되어 5σ 규칙을 활용하였다. σ값은 2020년 한 해 자료의 표준편차를 사용하였으며, 5σ 규칙에 적용될 자료는 잔차 및 잔차의 시간변동량이다. 두 번째로 적용한 방법은 이동평균(moving average 또는 moving window)과 경험적 규칙(3σ)을 접목하는 것이다. 윈도우(window)의 크기는 본 연구의 시점 설계와 동일한 조건으로 설정하기 위하여 전후 15분으로 하였다. 우선 원자료와 이동평균값으로부터의 차이를 아노말리(anomaly)로 정의하여 아노말리의 절대값이 3σ(변칙의 표준편차)를 넘는 경우를 이상치로 판별하도록 하였으며, 잔차의 시간변동량 또한 동일 윈도우에서의 3σ(변동량의 표준편차)를 넘는 경우 이상치로 판단하도록 하였다.
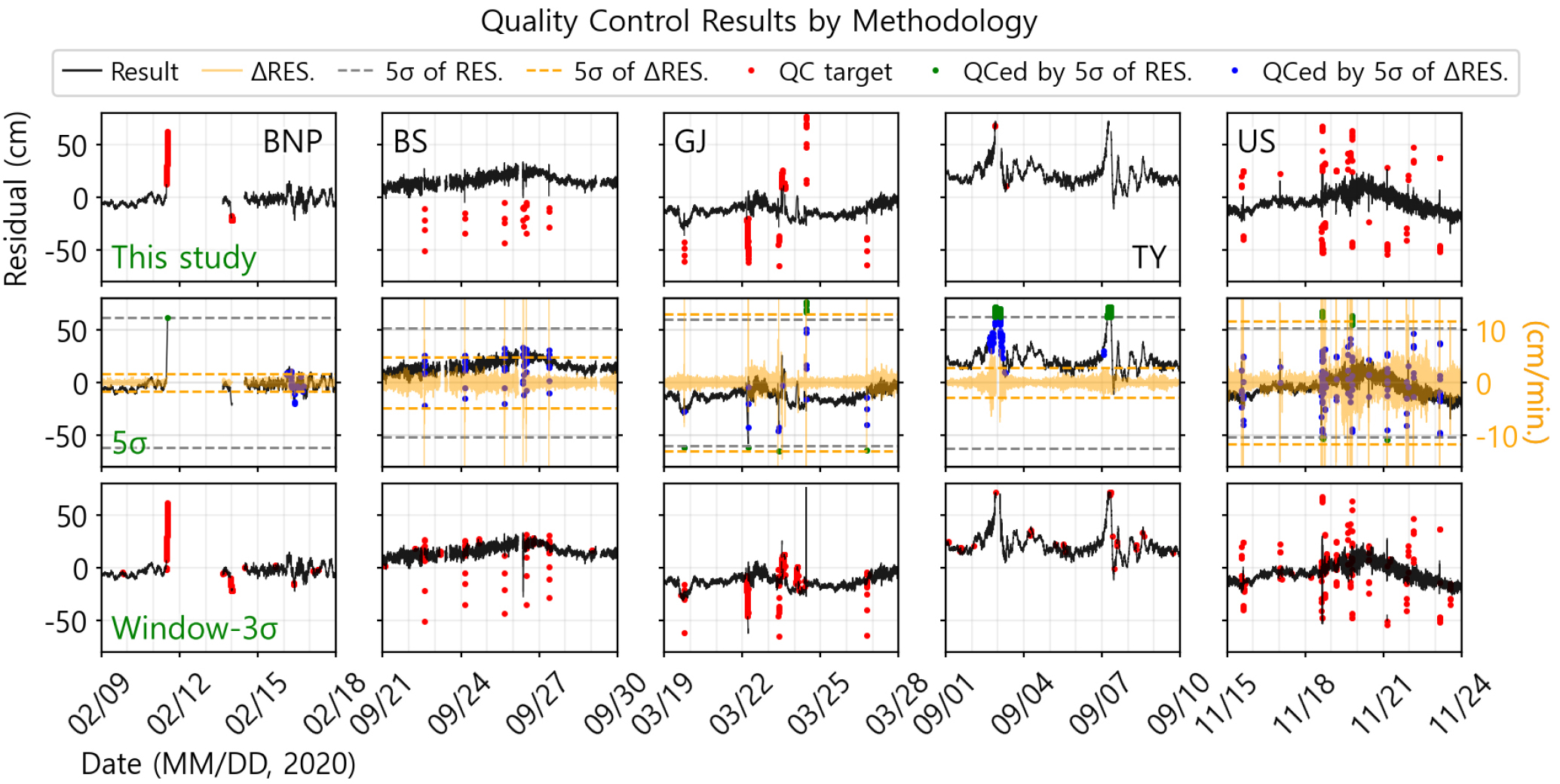
Fig. 12.
Quality control results from the three QC methods. The first row is the result of this study, the second row is an example of a 5sigma rule with a combination of the residuals and the time variations of the residuals, and the third row is an example of a 3sigma rule with a 31-minute window. The solid black line represents the quality-treated sea level value. The solid yellow line means the time variation of the residuals, and the dashed gray and yellow line means the 5σ of the residuals and the residual variation, respectively. The red dot is the target of QC, and the green and blue dot is the target of QC by the 5σ limit of residual and residual variations, respectively.
5σ 규칙을 활용했을 시에는 변동량 또한 활용하였기 때문에 단발적인 튐 값의 탐지는 잘 이루어지지만, 부산항신항과 거제도 조위관측소의 단조 증가 또는 감소중인 이상치는 오측으로 감지하지 못함을 볼 수 있으며, 통영 관측소의 이벤트 값은 과도하게 오측으로 판단한 것을 알 수 있다. 다음으로 이동평균 윈도우와 3σ 규칙을 함께 사용할 경우, 단순 5σ 규칙의 적용과는 달리 단조 증가 및 감소에 대한 분해능은 제고되었지만 단주기변동성이 오측으로 과하게 감지되며, 다발적인 오측이 나타나는 구간에서는 윈도우 내의 표준편차가 증가함으로 인해 분해능이 저해되는 것으로 나타났다. 살펴본 바와 같이 일반적인 품질처리 방법을 적용하여 이상치를 탐지해낼 때에는 여러 제약이 존재했지만, 본 연구의 모델을 적용할 시에는 앞서 언급한 영향을 받지 않고 이상치를 잘 탐지해 냄을 재차 확인할 수 있었다.
4.4 이상값 탐지 모델 개선방향
본 연구는 원자료를 활용하고 간단한 모델을 수립함으로써 준실시간 해수위 이상탐지를 가능하게 하였고, 해당 모델은 이상탐지 뿐만 아니라 장기간 자료의 품질처리 또한 가능하도록 설계되었다. 하지만 연구 수립 및 검토 과정에서 몇 가지 한계점을 확인하였다. 본 절에서는 앞 토의과정 중 논했던 것에 더하여 연구 또는 실무 현장에서 고려할 방향을 제안하고자 한다.
첫 번째는 정점별 특성의 고려이다. 본 연구는 문제의 단순화를 위해 전 정점에서 동일한 방법 및 모수(parameter)를 사용하였는데, 추가적인 자료의 분석이 진행된다면 각 정점에 최적화된 모수를 선정할 수 있을 것이다. 가장 먼저 고려될 수 있는 모수는 오차편차(σ)에 곱하는 값으로, 그 근거는 다음과 같다. 관측 자료와 모델이 추정한 자료의 전력 스펙트럼 밀도(power spectral density)를 비교하였을 때, 자료 간의 주파수대역별 에너지분위는 2시간 미만에서 상이하게 나타났는데, 공통적으로 모든 정점의 모델이 2시간 미만의 변동성을 잘 표현하지 못하고 있는 것을 확인하였다. 추가 연구 목적이 해수위의 재현이 아닌 이상, 정점별로 세분화된 모델 설계보다는 관측자료가 가지는 변동성을 고려한 모수 설계가 현실적인 방안으로 고려될 수 있을 것이다.
두 번째는 비지도학습과 지도학습의 병용이다. 본 연구의 모델은 이상치의 확률만을 제시하고 있으며, 이상치의 분류(classification)는 고려 대상이 아니었다. 하지만 이상치의 범주 또한 사용자에게 중요한 정보이므로 추가 연구에서는 이상치의 범주화 또한 주요 고려 대상이 될 수 있다. 많은 연구들이 데이터 범주화를 위해 지도학습을 사용한 분류모델을 수립해왔지만, 오측이 빈번하지 않은 자연시계열 자료는 데이터 불균형 이슈가 남아있다. 따라서 자료의 밀도추정, 즉 유사한 자료들의 군집화를 수행하는 비지도학습을 사용한다면 데이터 불균형 이슈를 피할 수 있을 것으로 예상한다. UNESCO(2013)는 품질표기(quality flag)를 두 단계에 걸쳐서 표기할 것을 제안하는데, 1차 품질표기로 데이터의 상태(e.g., good, not available, questionable, bad, missing data)를, 2차 품질표기로 품질처리 결과와 데이터 처리 이력(e.g., globally impossible values, spike, interpolated value, etc.)을 명시함으로써 1차 품질표기를 보완하도록 한다. 또한 GTSPP, SeaDataNet 등의 프로젝트에서 사용되고 있는 품질표기를 예시로 담아두었다. 이러한 선행연구 사례를 근거로 하여 품질처리 표기 범주들의 데이터특성을 고려한다면, 비지도-지도학습 연계 설계로 이상치 분류모델을 수립할 수 있을 것이다.
5. 요약 및 결론
본 연구는 남동해안에 위치한 5개 조위관측소에서의 해수위 준실시간 이상치 모니터링을 수행하였다. 지도학습 기법의 한계 중 하나인 데이터불균형을 역이용, 인근한 관측 정점들의 해수위 자료로 목표 정점의 해수위를 모의함으로써 이상치를 감지할 수 있도록 설계하였다. 해수위 성분인 잔차는 주변의 관측정점들과 시간 및 공간 상관성을 가지고 있음에 착안하여 앙상블 LSTM 모델세트를 설계하였고, 보팅(voting)을 통해 관측값의 오측 확률을 제시하였다. 또한 앙상블 과정에서 일부 정점에서의 부분결측에도 대응할 수 있는 구조를 만들었다.
목표 정점의 해수위 모의 결과, 평균 RMSE는 2.9~4.0 cm 로 모델이 검증되었으며, 해당 RMSE를 활용, 인 관측값을 이상치로 판별한 결과, 평시 및 기압점프, 태풍 통과 등 해양 이벤트시에서도 정상값과 오측값을 성공적으로 분리하였다. 이어서, 학습자료 연도 외의 자료를 활용, 상대적으로 짧은 기간의 학습으로도 장기간 자료에의 적용이 가능함을 보임으로써 인공신경망 기법의 장점인 가중치세트 재사용이 가능함을 확인하였다.
본 연구는 품질처리가 되지 않은 원자료를 사용하고, 간단한 구조의 모델을 설계함으로써 문제를 최대한 단순화한 과정과 결과를 제시하였는데, 그에 따라 발생할 수 있는 문제점들과 개선점들 또한 함께 제시하였다. 평시에 나타나는 오측 과적합은 품질처리 된 데이터를 사용하거나 앙상블 멤버를 늘리는 방안을, 이벤트시에 나타나는 과소적합은 기상자료의 추가로 문제를 완화하는 방안을 제시하였다. 모든 관측소에 대한 모델 설계가 획일화 되어있기 때문에 이를 특성화시키는 방안 또한 제시하였으며, 이상파랑 등의 전파속도 및 준실시간의 적합성을 고려한 순차 길이 선정 또한 제안하였다.
연구 설계 과정을 간소화했음에도, 본 연구의 모델은 일반적인 품질처리나 이상치 모니터링 방법보다 더 우수한 오측 분해능을 보여주었다. 따라서, 제시한 개선방향과 함께 밀집된 주변 관측소의 데이터를 추가로 확보할 경우, 더욱 성능이 더욱 향상될 것이 기대된다. 마지막으로, 본 연구의 이상치 탐지 알고리즘은 해수위에 한정되지 않기 때문에 많은 해양 및 대기자료의 이상치 탐지 및 품질처리에 확장 적용될 수 있을 것으로 기대된다.